Question

If a tower ${\text{30 m}}$ high, cause a shadow $10\sqrt 3$ long on the ground, and then find the angle of elevation of the sun.

Answer 1

Hint : We can use the concept of trigonometric ratio. Draw the diagram and find which ratio will help to solve the question.
Formula Required: ${tan\theta} = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}}$
$\tan {60^ \circ } = \sqrt 3$

Complete step-by-step answer :
Given: Height of the tower is ${\text{30m}}$
Length of the shadow casted by the tower on the ground is $10\sqrt 3$
We need to find the angle of elevation of the sun.
Consider the below figure,

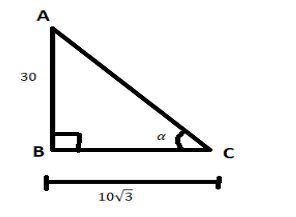
${\text{AB}}$ is the height of the tower
${\text{BC}}$ is the length of the shadow casted by the tower on the ground
${\alpha }$ is the angle of elevation of the sun
From the above figure we see that the opposite side and adjacent sides to the angle of elevation is given,
We can use tan ratio.
As we know that ${tan\theta} = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}}$
$\Rightarrow {tan\alpha} = \dfrac{{{\text{opposite side }}}}{{{\text{adjacent side}}}}$
$\Rightarrow tan\alpha = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}$
$\Rightarrow \tan \alpha = \dfrac{{30}}{{10\sqrt 3 }} \\\ \Rightarrow \tan \alpha = \dfrac{3}{{\sqrt 3 }} \\\ \Rightarrow \tan \alpha = \sqrt 3 \\\$
Since $\tan {60^ \circ } = \sqrt 3$
$\tan\alpha = {tan6}{{\text{0}}^{\text{o}}} \\\ \Rightarrow \alpha = {6}{{\text{0}}^{\text{o}}} \;$
Therefore, the angle of elevation of the sun is ${60^ \circ }$ .
So, the correct answer is “ ${60^ \circ }$”.

Note : In the questions involving heights and distances concept the diagram leads to forming right triangles, In that case the questions tests us about the trigonometric ratios. We need to have an idea about the definition of trigonometric ratios and the values of angle of the same . As per the data given in the question we need to figure out which ratio will help us to find the answer.