Question

If a tower is 30m high, casts a shadow of $10\sqrt{3}m$ long on the ground, then finds the value of angle of elevation of sun?

Answer 1

Hint: The tower, the shadow and the line joining the top of the tower to the end of the shadow constructs a right angled triangle. We know the length of the base and the height of the triangle then using $\tan \theta$, we can find the angle of elevation of the sun.

Complete step-by-step answer:
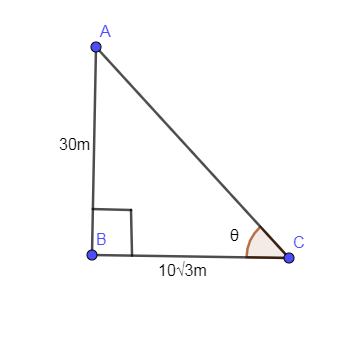
It is given that the height of the tower is 30m and the length of the shadow is $10\sqrt{3}m$.
The below diagram is showing the height of the tower (AB), the shadow of the tower (BC) and angle of inclination of the sun is given by $\theta$.

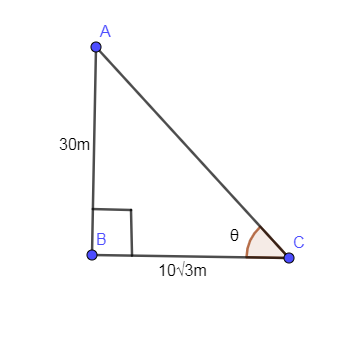
In the above right angled triangle, right angled at B,
$\tan \theta =\dfrac{P}{B}$
In the above formula, “P” stands for perpendicular corresponding to angle $\theta$ and “B” stands for the base corresponding to angle $\theta$ so using this formula in the above triangle.
In the above triangle, $P=30m;B=10\sqrt{3}m$so substituting these values in the above equation we get,
$\begin{aligned} & \tan \theta =\dfrac{30}{10\sqrt{3}} \\\ & \Rightarrow \tan \theta =\dfrac{3}{\sqrt{3}}=\sqrt{3} \\\ \end{aligned}$
We know that, $\tan \theta =\sqrt{3}$ when $\theta ={{60}^{0}}$ so the above equation is reduced to:
$\theta ={{60}^{0}}$
From the above solution, we have found the angle of elevation of the sun is ${{60}^{0}}$.
Note: The point to be noted here is that the shadow lies on the floor so the shadow in the diagram is BC not AC. You might get confused that the shadow is AC but it is BC and the angle of elevation of the sun is $\angle ACB$ not $\angle BAC$.