Solveeit Logo
Login

Question

Question: If a tangent to the circle \({{x}^{2}}+{{y}^{2}}=1\) intersects the coordinate axes at distinct poin...

If a tangent to the circle x2+y2=1{{x}^{2}}+{{y}^{2}}=1 intersects the coordinate axes at distinct points P and Q, then the locus of the midpoint of PQ is?
(a) x2+y2−2xy=0{{x}^{2}}+{{y}^{2}}-2xy=0
(b) x2+y2−16x2y2=0{{x}^{2}}+{{y}^{2}}-16{{x}^{2}}{{y}^{2}}=0
(c) x2+y2−4x2y2=0{{x}^{2}}+{{y}^{2}}-4{{x}^{2}}{{y}^{2}}=0
(d) x2+y2−2x2y2=0{{x}^{2}}+{{y}^{2}}-2{{x}^{2}}{{y}^{2}}=0

Explanation

Solution

Hint: First we will assume the mid point and then its coordinates. Then we will find the coordinates of the point P and Q through which the line is passing and then using the equation of line i.e. OQ=xh+yk=rOQ=\dfrac{x}{h}+\dfrac{y}{k}=rand equation of circle i.e. x2+y2=a2{{x}^{2}}+{{y}^{2}}={{a}^{2}} we will find the final equation of locus of midpoint of PQ.

Complete step-by-step answer:
In question it is given that a tangent to the circle x2+y2=1{{x}^{2}}+{{y}^{2}}=1 intersects the coordinate axes at distinct points P and Q, so, on basis of it we will draw the figure for our simplicity,

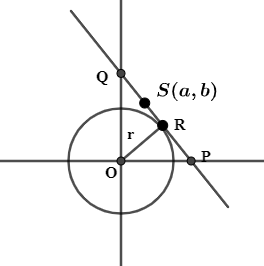
Now, from the figure we can assume a point S as a mid point of locus PQ and then we will assume the coordinates of mid point as S(a,b)S\left( a,b \right),
Now, the coordinates of P and Q can be given as,
P(2a,0)P\left( 2a,0 \right) and Q(0,2b)Q\left( 0,2b \right)
Now, the equation of line passing through two points can be given by,
OQ=xh+yk=rOQ=\dfrac{x}{h}+\dfrac{y}{k}=r ……………..(i)
Where, h is coordinate of x and k is coordinate of y and r is the radius of the circle.
Here, from the equation of circle given i.e. x2+y2=1{{x}^{2}}+{{y}^{2}}=1 by comparing it with the equation of circle which can be given as,
x2+y2=a2{{x}^{2}}+{{y}^{2}}={{a}^{2}} ………………..(ii)
So, by comparing the equations we can say that the radius of the circle is 1 unit.
Now, the expresion (i) in terms of coordinates of P and Q can be given as,
PQ=x2a+y2b=1PQ=\dfrac{x}{2a}+\dfrac{y}{2b}=1 …………………..(iii)
Now, the equation of line perpendicular to the radius of circle can be given as,
OR=∣−1(1a)2+(1b)2∣OR=\left| \dfrac{-1}{{{\left( \dfrac{1}{a} \right)}^{2}}+{{\left( \dfrac{1}{b} \right)}^{2}}} \right|, where a and b are values of coordinates of x and y.
Now we know that value of radius is 1 s on substituting the values and comparing it with value of radius we will get,
OR=∣−1(12a)2+(12b)2∣=1OR=\left| \dfrac{-1}{{{\left( \dfrac{1}{2a} \right)}^{2}}+{{\left( \dfrac{1}{2b} \right)}^{2}}} \right|=1
⇒14a2+14b2=1⇒4a2+4b24a2⋅4b2=1\Rightarrow \dfrac{1}{4{{a}^{2}}}+\dfrac{1}{4{{b}^{2}}}=1\Rightarrow \dfrac{4{{a}^{2}}+4{{b}^{2}}}{4{{a}^{2}}\cdot 4{{b}^{2}}}=1
⇒4a2+4b2=4a2⋅4b2\Rightarrow 4{{a}^{2}}+4{{b}^{2}}=4{{a}^{2}}\cdot 4{{b}^{2}}
⇒a2+b2=4a2⋅4b24⇒a2+b2=4a2b2\Rightarrow {{a}^{2}}+{{b}^{2}}=\dfrac{4{{a}^{2}}\cdot 4{{b}^{2}}}{4}\Rightarrow {{a}^{2}}+{{b}^{2}}=4{{a}^{2}}{{b}^{2}}
Now, converting the equation in form of x and y, the equation can be written as,
x2+y2=4x2y2{{x}^{2}}+{{y}^{2}}=4{{x}^{2}}{{y}^{2}}
⇒x2+y2−4x2y2=0\Rightarrow {{x}^{2}}+{{y}^{2}}-4{{x}^{2}}{{y}^{2}}=0
Thus, the equation of locus of mid point of line PQ is x2+y2−4x2y2=0{{x}^{2}}+{{y}^{2}}-4{{x}^{2}}{{y}^{2}}=0.
Hence, option (c) is the correct answer.

Note: Remember over here in this sum values of all the coordinates of x and y of point S were positive so incase if we substitute the values of x in y or vice-versa i.e. OR=∣−1(12b)2+(12a)2∣=1OR=\left| \dfrac{-1}{{{\left( \dfrac{1}{2b} \right)}^{2}}+{{\left( \dfrac{1}{2a} \right)}^{2}}} \right|=1, the final answer does not change as everything is positive. But, if we consider negative coordinates in other sums then changes may come in answer so students must be careful while solving such problems.