Question
Question: If \[A\subset B,n\left( A \right)=5\] and \[n\left( B \right)=7\], then \[n\left( A\cup B \right)=\]...
If A⊂B,n(A)=5 and n(B)=7, then n(A∪B)=_ _ _ _ _ _ _ _ _.
(a) 5
(b) 7
(c) 2
(d) 12
Solution
Hint: Use the formula for union of two sets that is n(A∪B)=n(A)+n(B)−n(A∩B). Now, since A⊂B, therefore put n(A∩B)=n(A), then use the given information that is n(A)=5 and n(B)=7.
Here, we are given two sets A and B such that A⊂B, n(A)=5 and n(B)=7. We have to find the value of n(A∪B).
Before proceeding with the question, we must know some of the terminologies related to sets.
First of all, a ‘set’ is a collection of well-defined and distinct objects. The most basic property of a set is that it has elements. The number of elements of a set, say A is shown by n(A).
Here, in the question we have n(A)=5 and n(B)=7, that means the number of elements in set A is 5, while the number of elements in set B is 7.
Now, a ‘subset’ is a set which is contained in another set. We can also put it as, if we have a set P which is a subset of another set Q, then P is contained in Q as all the elements of set P are elements of Q. This relationship is shown by P⊂Q.
We can show it diagrammatically as,
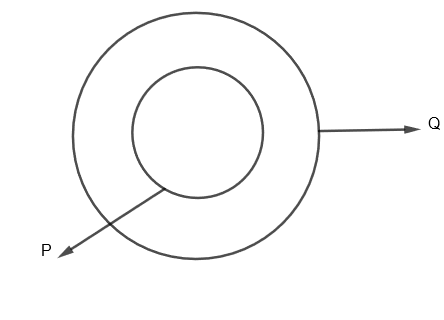
Here, P⊂Q, that means P is contained in Q as P is a subset of Q.
In question, we are given that A⊂B, that means that A is a subset of B or A is contained in B. We can show them as
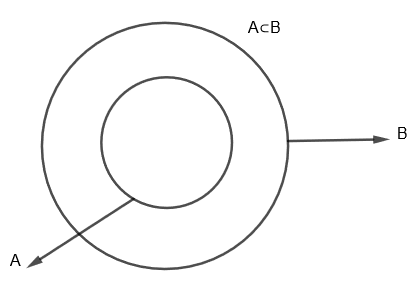
Now, union of two sets say P and Q is the set of elements which are in P, in Q or both P and Q. For example, if P = {1, 3, 5, 7} and Q = {1, 2, 4, 6, 7}, then union of P and Q which is shown as P\cup Q=\left\\{ 1,2,3,4,5,6,7 \right\\}
Diagrammatically, the shaded portion is P∪Q which is as follows
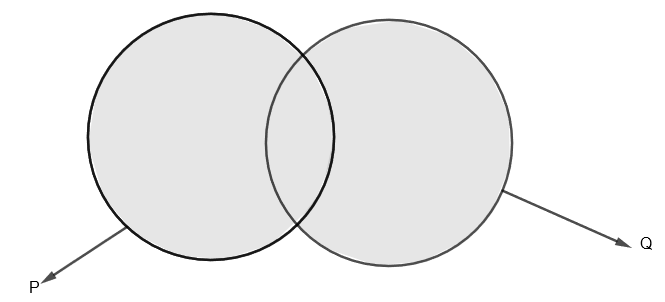
The formula for n(P∪Q)=n(P)+n(Q)−n(P∩Q).
Here, P∩Q is the area common to both P and Q.
Now, in the given question, we have to find n(A∪B), that is, the number of elements in A union B.
We can show A∪B by a shaded portion which is as follows.
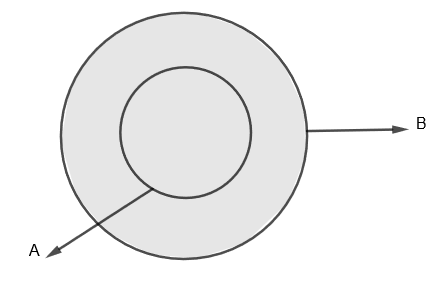
Here, A⊂B and n(A)=5 and n(B)=7.
Here, we can see that the portion common to the set A and B that is (A∩B) is nothing but set A. Therefore, here we have n(A∩B)=n(A)=5.
As we know that n(P∪Q)=n(P)+n(Q)−n(P∩Q), therefore to get n(A∪B), we will put A and B in place of P and Q respectively, we will get
n(A∪B)=n(A)+n(B)−n(A∩B)
Since, we have found that n(A∩B)=n(A)=5.
Therefore we get, n(A∪B)=n(A)+n(B)−n(A)
By putting the values of n (A) and n (B), we get,
n(A∪B)=5+7−5
n(A∪B)=7
Therefore, we get n(A∪B)=7
Hence, option (b) is correct.
Note: Students must note that whenever A⊂B, that is A is subset of B, then n(A∪B), that is the number of elements in A union B is equal to number of elements in set B that is, n(A∪B)=n(B) when A⊂B. Also, some students make this mistake of writing n(A∪B)=n(A)+n(B) which is wrong. They must remember to subtract n(A∩B) as well. Hence, n(A∩B)=n(A)+n(B)−n(A∩B).
