Question

If a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then

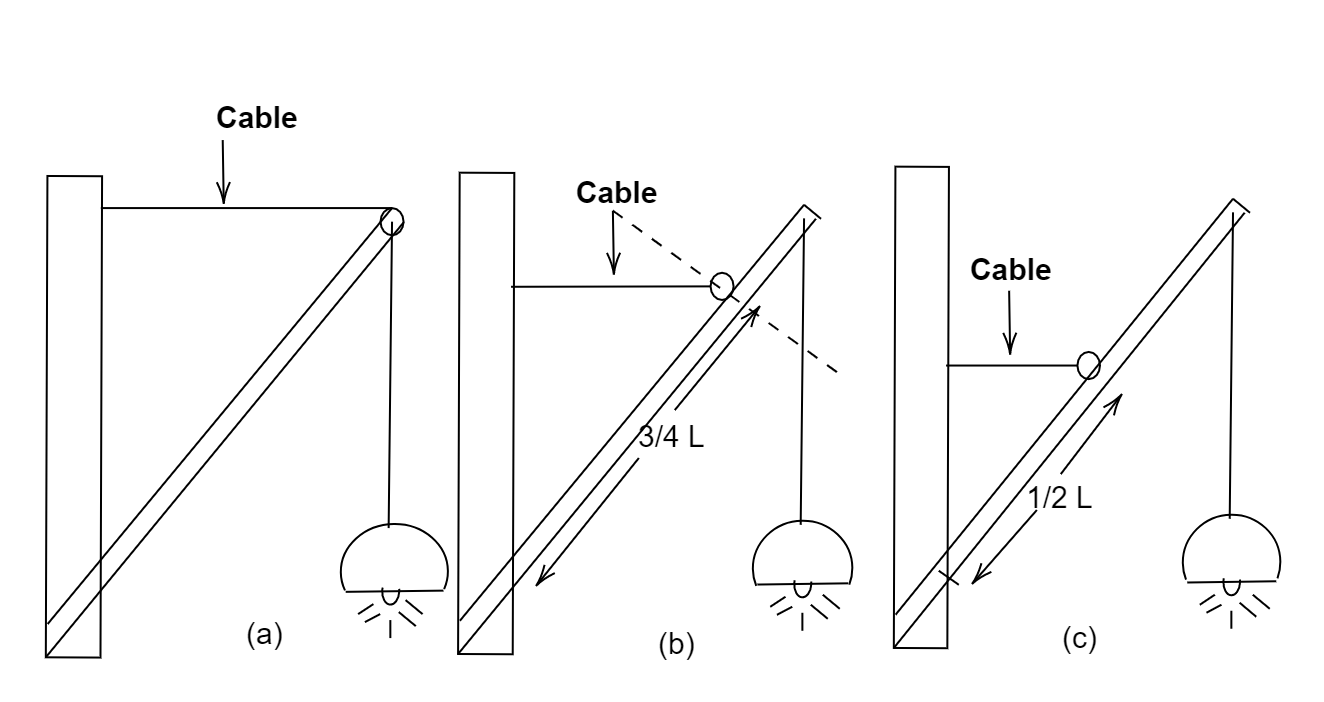
(A) Pattern A is more sturdy
(B) Pattern B is more sturdy
(C) Pattern C is more sturdy
(D) All will have same sturdiness

Answer 1

Here we need to calculate the sturdiness in all the three cases. In all the three cases the torque due to gravitational force that is mg is balanced by the torque due to tension. In order to compare the sturdiness we have to check in which case torque due to tension is maximum, that case is more sturdy.

Complete step by step solution:
We are given three cases where three different positions of cable are shown.
From this figure we can say that,
Torque created due to weight, that is mg, of the street light remains the same for all the three cases. This torque due to weight is balanced by the torque created by tension in the string. Torque due to tension is calculated as the magnitude of tension multiplied with the perpendicular distance from the line of action of tension to the axis of rotation. So if $\tau$ be the torque and $T$ be tension in the string and $L$ be perpendicular distance of cable from the axis of rotation then,
$\tau = T \cdot d$
Tension is same in all the three cases, so the perpendicular distance between the line of action of tension to the axis of rotation in which case it is maximum is more sturdy. Now from the figure we can see that in case A the perpendicular distance is maximum but in other two cases it is less than case A.
Therefore the correct option is (A) Pattern A is more sturdy.

Note:
Always keep in mind when torque is maximum then the system is said to be more sturd. Another important thing is when tension remains constant then the torque due to tension will be directly proportional to the perpendicular distance between the line of action of tension to the axis of rotation. Hence when distance increases the torque also increases.