Question

If a straight line passing through the point $P\left( -3,4 \right)$ is such that it is intercepted portion between the coordinates axes is bisected at $P$ , then its equation is:
(a) $x-y+7=0$
(b) $3x-4y+25=0$
(c) $4x+3y=0$
(d) $4x-3y+24=0$

Answer 1

First , we will locate the point $P\left( -3,4 \right)$ in a graph and then try to make a line which is passing through $P$ and has intercepts at the coordinate axis . Use the general intercept form of a line i.e. $\dfrac{x}{a}+\dfrac{y}{b}=1$ , and then use the condition that $P$ is bisecting the intercepted portion and hence find the value of intercepts $a$ and $b$ . Putting the value of these intercepts in the general form , we get the desired equation.

Complete step-by-step answer:
First , we will will location the point $P\left( -3,4 \right)$ in a graph

Now, the line passing through $P$ with intercept at $x$ be $a$ and at $y$ be $b$ , will look like

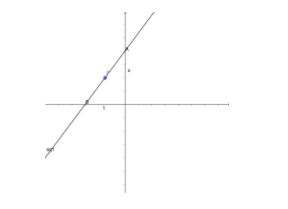
We know that the general equation having $x$ - intercept as $a$ and $y$ - intercept as $b$ is
$\dfrac{x}{a}+\dfrac{y}{b}=1$
Now, as mentioned in the question that the point $P$ bisects the intercepted portion between coordinate axis , it means the point $P$ bisects the line $AB$
$\begin{aligned} & \Rightarrow P=\left( \dfrac{a}{2},\dfrac{b}{2} \right)=\left( 3,-4 \right) \\\ & \Rightarrow \left( a,b \right)=\left( -6,8 \right) \\\ \end{aligned}$
Hence, we can now put these constants to the general form and get the desired equation,
$\begin{aligned} & \dfrac{x}{a}+\dfrac{y}{b}=1 \\\ & \dfrac{x}{-6}+\dfrac{y}{8}=1 \\\ & 8x-6y=-48 \\\ & 4x-3y+24=0 \end{aligned}$
Hence , the desired equation is $4x-3y+24=0$ .

So, the correct answer is “Option d”.

Note: The probability of mistake here is that student might at first let the general form as the general equation of straight line i.e. $ax+by=c$ , assuming this is not wrong but the condition given in the question involves intercepts , so we have to let the general form where constants , involves the intercepts of coordinate axis.