Question

If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight angles, if produced indefinitely, meet on the other side on which the sum of angles is less than two right angles.

Answer 1

In order to prove the given statement, we will be considering one base line and two lines falling on the baseline such that it can be produced such that it meets at one side only. Then upon assuming the measurements of the angles, we can prove the given statement.

Complete step by step answer:
Now let us state the statements of Euclid’s postulates:
1.A straight line segment can be drawn joining any two points.
2.Any straight line segment can be extended indefinitely in a straight line.
3.Given any straight lines segment, a circle can be drawn having the segment as radius and one endpoint as centre.
4.All Right Angles are congruent.
5.If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two Right Angles, then the two lines inevitably must intersect each other on that side if extended far enough.
Now let us prove the given statement by step by step.
If a straight line falls on two straight lines;

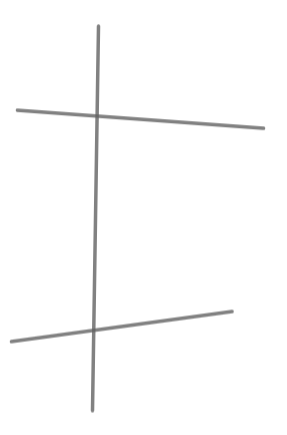
It makes the interior angles on the same side less than two right angles.

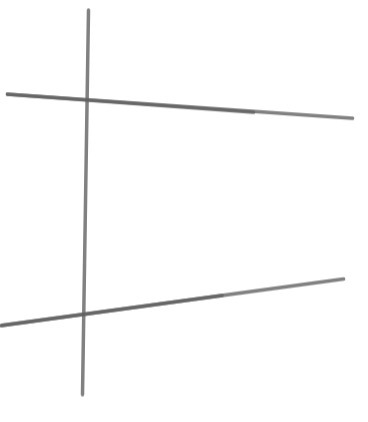
Now, the two straight lines produced indefinitely, meet on that side on which the angles are less than two right angles.

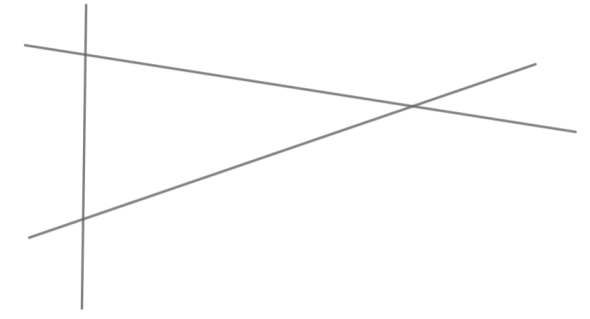
Hence we have proved the given statement.

Note: We must have an assumption of the figure according to the statement given. We can only prove this only if we produce the straight lines but we must know to which side the lines are to be produced. If we produce the lines on the other side then we get the sum of angles greater than two right angles.