Question

If a simple pendulum has a significant amplitude (up to a factor of 1/e of original) only in the period between $t=0s$ to $t=\tau s$, then ‘$\tau$’ may be called the average life of the pendulum. When the spherical Bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with ‘b’ as the constant of proportionality, the average lifetime of the pendulum (assuming damping is small) in seconds
$\begin{aligned} & \text{A}\text{. }\dfrac{0.693}{b} \\\ & \text{B}\text{. }b \\\ & \text{C}\text{. }\dfrac{1}{b} \\\ & \text{D}\text{. }\dfrac{2}{b} \\\ \end{aligned}$

Answer 1

We are given the significant amplitude between a time period of a simple pendulum and also said that the retardation of the bob is proportional to a constant. We can solve the question by finding the general solution for the damped simple pendulum. Then by comparing it with the equation for linear displacement, we will get the solution.

Formula used: $\tau =\vec F\times {\vec{r}_{\bot }}$
$\tau =I\alpha$
$I=m{{l}^{2}}$

Complete step by step answer:
In the question we have a simple pendulum.
It is said that the pendulum has a significant amplitude only when the time period of the pendulum is between $t=0s\text{ and }t=\tau s$. Here ‘$\tau$’ is the average life of the pendulum.
Consider the figure of a simple pendulum given below.

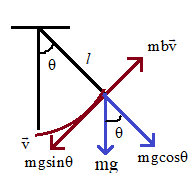
From the figure we can see that the restoring force of the pendulum is $mg\sin \theta$, which is directed against the mean position.
From this question we know that this restoring force is opposed by the damping force, i.e.
Effective force, $F=mg\sin \theta -mb\vec{v}$
Since the restoring force is an opposing force, we get the effective restoring force as,
$\Rightarrow F=-\left( mg\sin \theta -mb\vec{v} \right)$
Now let us calculate the torque in the system. We know that torque is the cross product of force and perpendicular distance, i.e.
$\tau =\vec F\times {\vec{r}_{\bot }}$
We know that the perpendicular distance here is ‘$l$’. Therefore,
$\Rightarrow \tau =F\times l$
$\Rightarrow \tau =Fl\sin \theta$
Since it is perpendicular, we have $\theta =90{}^\circ$
$\Rightarrow \tau =Fl\sin 90$
$\Rightarrow \tau =Fl$
Since, $F=-\left( mg\sin \theta -mb\vec{v} \right)$, we get
$\Rightarrow \tau =-\left( mg\sin \theta -mb\vec{v} \right)l$
We know that torque is also described as,
$\tau =I\alpha$, where ‘$I$' is the moment of inertia and ‘$\alpha$’ is angular acceleration.
We know that here the moment of inertia of the pendulum is,
$I=m{{l}^{2}}$
Therefore we get, $\Rightarrow \tau =m{{l}^{2}}\alpha$
Now we can equate the two equations for torque in this system. Thus we get,
$\Rightarrow m{{l}^{2}}\alpha =-\left( mg\sin \theta -mb\vec{v} \right)l$
By solving this we get,
$\Rightarrow m{{l}^{2}}\alpha =-ml\left( g\sin \theta -b\vec{v} \right)$
$\Rightarrow l\alpha =-g\sin \theta +b\vec{v}$
Here we know that, ‘$\alpha$’ the angular acceleration is the rate of change of angular velocity with time and the angular velocity is the rate of change of the angle with respect to time. Therefore we can write,
$\vec{v}=\dfrac{d\theta }{dt}$
$\alpha =\dfrac{d\vec{v}}{dt}$
$\Rightarrow \alpha =\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}$
By substituting these values for angular acceleration and angular velocity, we will get
$\Rightarrow l\times \dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}=-g\sin \theta +b\dfrac{d\theta }{dt}$
$\Rightarrow \dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}=\dfrac{-g\sin \theta }{l}+\dfrac{bd\theta }{ldt}$
This is the differential equation for damped oscillation in terms of the angle.
The general solution for this differential equation is,
$\theta ={{\theta }_{0}}{{e}^{{}^{-bt}\\!\\!\diagup\\!\\!{}_{2}\;}}\sin \left( \omega t+\phi \right)$
We know that the displacement in a damped oscillation is given as,
$x=A\sin \omega t$
Comparing this with the general solution we can see that,
$A={{\theta }_{0}}{{e}^{{}^{-bt}\\!\\!\diagup\\!\\!{}_{2}\;}}$
This is the angular amplitude.
In the question it is given that the angular amplitude after ‘$\tau$’ time will become $\left( \dfrac{1}{e} \right)$. Therefore we can write,
$\Rightarrow {{\theta }_{0}}{{e}^{{}^{-b\tau }\\!\\!\diagup\\!\\!{}_{2}\;}}=\dfrac{{{\theta }_{0}}}{e}$
$\Rightarrow {{e}^{{}^{-b\tau }\\!\\!\diagup\\!\\!{}_{2}\;}}=\dfrac{1}{e}$
$\Rightarrow \dfrac{b\tau }{2}=1$
$\Rightarrow \tau =\dfrac{2}{b}$
Therefore we get the average life time of the pendulum as $\dfrac{2}{b}$.

So, the correct answer is “Option C”.

Note: A simple pendulum consists of a point mass suspended on a weightless inextensible perfectly flexible thread and it is free to vibrate without any effect of friction. Damping is any kind of force that reduces the amplitude of the vibration. When an oscillation is affected by any damping force then that oscillation is a damped oscillation.