Solveeit Logo
Login

Question

Question: If a polynomial P(x) given by $P(x)=2x^4+ax^3+bx^2+cx+d$ is such that P(1) = 4, P(2) = 7, P(3) = 12 ...

If a polynomial P(x) given by P(x)=2x4+ax3+bx2+cx+dP(x)=2x^4+ax^3+bx^2+cx+d is such that P(1) = 4, P(2) = 7, P(3) = 12 and P(4) = 19, then P(5) =

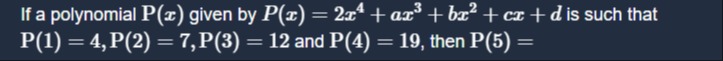
Answer

76

Explanation

Solution

We are given

P(x)=2x4+ax3+bx2+cx+dP(x) = 2x^4 + ax^3 + bx^2 + cx + d

with

P(1)=4,P(2)=7,P(3)=12,P(4)=19.P(1)=4,\quad P(2)=7,\quad P(3)=12,\quad P(4)=19.

Define

R(x)=P(x)−2x4,R(x)=P(x)-2x^4,

so that R(x)R(x) is a cubic polynomial. Its values are:

xR(x)=P(x)−2x414−2(14)=4−2=227−2(16)=7−32=−25312−2(81)=12−162=−150419−2(256)=19−512=−493\begin{array}{c|c} x & R(x)=P(x)-2x^4 \\ \hline 1 & 4-2(1^4)=4-2=2\\[5mm] 2 & 7-2(16)=7-32=-25\\[5mm] 3 & 12-2(81)=12-162=-150\\[5mm] 4 & 19-2(256)=19-512=-493 \end{array}

Now, calculate the finite differences:

  • 1st Differences:

    Δ1=R(2)−R(1)=−25−2=−27,Δ2=R(3)−R(2)=−150−(−25)=−125,Δ3=R(4)−R(3)=−493−(−150)=−343.\begin{aligned} \Delta_1&=R(2)-R(1)=-25-2=-27,\\[5mm] \Delta_2&=R(3)-R(2)=-150-(-25)=-125,\\[5mm] \Delta_3&=R(4)-R(3)=-493-(-150)=-343. \end{aligned}

  • 2nd Differences:

    Δ12=Δ2−Δ1=−125−(−27)=−98,Δ22=Δ3−Δ2=−343−(−125)=−218.\begin{aligned} \Delta^2_1&=\Delta_2-\Delta_1=-125-(-27)=-98,\\[5mm] \Delta^2_2&=\Delta_3-\Delta_2=-343-(-125)=-218. \end{aligned}

  • 3rd Difference:

    Δ3=Δ22−Δ12=−218−(−98)=−120.\Delta^3 = \Delta^2_2-\Delta^2_1 = -218 - (-98) = -120.

    (For a cubic polynomial, this third difference is constant.)

Extrapolating to x=5x=5:

  1. Next 2nd difference: Δ32=Δ22+Δ3=−218+(−120)=−338.\Delta^2_3 = \Delta^2_2 + \Delta^3 = -218 + (-120) = -338.
  2. Next 1st difference: Δ4=Δ3+Δ32=−343+(−338)=−681.\Delta_4 = \Delta_3 + \Delta^2_3 = -343 + (-338) = -681.
  3. Value at x=5x=5: R(5)=R(4)+Δ4=−493+(−681)=−1174.R(5)= R(4)+\Delta_4 = -493 + (-681) = -1174.

Finally, recover P(5)P(5):

P(5)=R(5)+2(54)=−1174+2(625)=−1174+1250=76.P(5)= R(5)+2(5^4)= -1174 + 2(625) = -1174 + 1250 = 76.