Question

If a point $P$ be (-4, 0) such that the chord of contact of the pair of tangents from $P$ to the parabola $y^2=32x$ is $AB$.

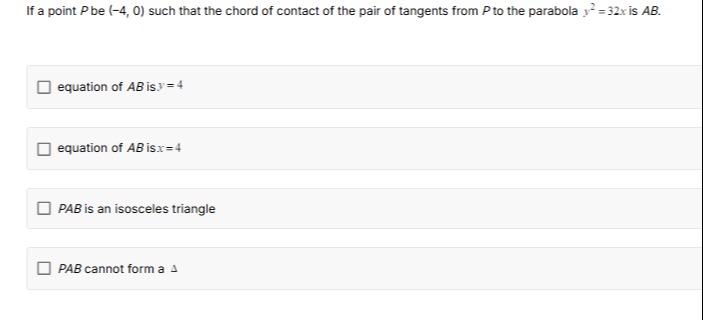
• A. equation of $AB$ is.$y=4$
• B. equation of $AB$ is $x=4$
• C. $PAB$ is an isosceles triangle
• D. $PAB$ cannot form a $\triangle$

Answer 1

Answer: (B), (C)

Equation of $AB$ is $x=4$ and $PAB$ is an isosceles triangle

Answer 2

Solution

1. For the parabola $y^2=32x$, we have $4a=32 \Rightarrow a=8$. The equation of the chord of contact from a point $(x_1,y_1)$ is given by:

   $$yy_1 = 2a(x+x_1)$$

2. For $P=(-4,0)$, substitute $x_1=-4$ and $y_1=0$:

   $$y\cdot 0 = 16(x-4) \Rightarrow 0=16(x-4) \Rightarrow x=4.$$

   So, the chord of contact $AB$ is the vertical line $x=4$.

3. The points of contact $A$ and $B$ are obtained by substituting $x=4$ in $y^2=32x$:

   $$y^2 = 32(4)=128 \Rightarrow y = \pm 8\sqrt{2}.$$

   So, $A=(4,8\sqrt{2})$ and $B=(4,-8\sqrt{2})$.

4. The distances:

   $$PA = \sqrt{(4 - (-4))^2 + \left(8\sqrt{2} - 0\right)^2} = \sqrt{8^2+(8\sqrt{2})^2} = \sqrt{64+128} = \sqrt{192} = 8\sqrt{3}.$$

   Similarly, $PB = 8\sqrt{3}$. Hence, $\triangle PAB$ is isosceles.

Explanation (Minimal):

• For $y^2=32x$, $a=8$; chord of contact from $(-4,0)$ gives $0=16(x-4)$ $\Rightarrow x=4$.

• Intersection with parabola: $y^2 = 128 \Rightarrow y=\pm 8\sqrt{2}$.

• Distances $PA$ and $PB$ are equal, so $\triangle PAB$ is isosceles.