Question

If a piece of metal is heated to temperature $\theta$ and then allowed to cool in a room which is at temperature ${\theta _0}$, the graph between the temperature T of the metal and time t will be closed to:
A.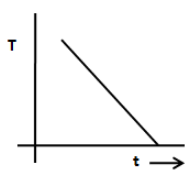

B.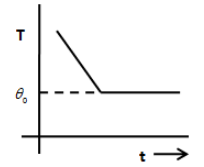

C.

D.

Answer 1

Recall Newton’s law of cooling and express the heat lost by the piece of metal. As the temperature decreases, the piece of metal will lose the heat energy. Express the heat energy loss in terms of temperature difference. Using the two equations you get, find the relation between the initial temperature and surrounding temperature with respect to the time.

Formula used:
$\dfrac{{dQ}}{{dt}} = k\left( {{T_1} - {T_0}} \right)$
Here, k is the constant, ${T_1}$ is the temperature of the substance and ${T_0}$ is the temperature of the surrounding.

Complete step by step answer:
We have from Newton’s law of cooling, the rate of loss of heat from the material is directly proportional to the difference in the temperature of the material and temperature of the surrounding. Therefore, we can write,
$\dfrac{{dQ}}{{dt}} = k\left( {{T_1} - {T_0}} \right)$ …… (1)
Here, k is the constant, ${T_1}$ is the temperature of the metal and ${T_0}$ is the temperature of the surrounding.

We have from the heat loss by the body as a function of temperature is given as,
$dQ = - mcdT$
Here, m is the mass of the metal piece and c is the specific heat of the metal and $dT$ is the difference in the temperature.
Dividing the above equation by $dt$, we get,
$\dfrac{{dQ}}{{dt}} = - mc\dfrac{{dT}}{{dt}}$ …… (2)

Comparing equation (1) and (2), we get,
$- mc\dfrac{{dT}}{{dt}} = k\left( {{T_1} - {T_0}} \right)$
$\Rightarrow \dfrac{{dT}}{{{T_1} - {T_0}}} = - \dfrac{k}{{mc}}dt$
$\Rightarrow \dfrac{{dT}}{{{T_1} - {T_0}}} = - Kdt$
Here, $K = \dfrac{k}{{mc}}$.

Integrating the above equation, we get,
${\ln _e}\left( {{T_1} - {T_0}} \right) = - Kt + C$
Here, C is the constant of proportionality.

We can rearrange the above equation as,
${T_1} - {T_0} = {e^{ - Kt}}{e^C}$
$\Rightarrow {T_1} = {T_0} + C'{e^{ - Kt}}$
Here, $C' = {e^C}$.
From the above equation, we can say that the graph between temperature T and time is an exponential decay graph and therefore, the option A and B are incorrect. The option D does not show an exponential decay graph. Therefore, the option D is incorrect.

So, the only correct answer is option C.

Note: The heat loss or gained by the substance is expressed as, $\Delta Q = mc\Delta T$. Whenever there is a decrease in the temperature, the heat is lost by the substance and if there is an increase in the temperature, the heat is gained by the substance. The heat gained has positive sign for $\Delta Q$ and heat loss has negative sign for $\Delta Q$.