Question

If a perpendicular is drawn from the vertex containing the right angle of a right-angled triangle to the hypotenuse then prove that the triangles on each side of the perpendicular are similar. Also, prove that the square of the length of the perpendicular is equal to the product of the two parts of the hypotenuse.

Answer 1

Hint: Use the fact that if one angle of a right-angled triangle (other than the right angle) is x, then the other angle is $90{}^\circ -x$. Hence prove that $\angle ACD=\angle DAB$ and $\angle DAC=\angle ABD$. Hence prove that the triangles are similar using A.A.A. similarity criterion. Hence prove that $\dfrac{AD}{CD}=\dfrac{BD}{AD}$ using the properties of similar triangles and hence prove that $A{{D}^{2}}=DC\times BD$

Complete step-by-step answer:
Given: ABC is a right-angled triangle, right-angled at A and AD is perpendicular to side BC

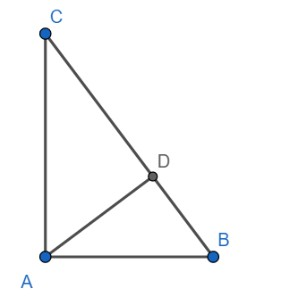
To prove :
[i] Triangles ADB and CDA are similar
[ii] $A{{D}^{2}}=CD\times DB$
Proof:
Let $\angle ABD=x$
We know that if one angle of a right-angled triangle (other than the right angle) is x, then the other angle is $90{}^\circ -x$
Hence, we have $\angle DAB=90{}^\circ -x$
Now, we have
$\angle BAC=\angle BAD+\angle DAC$
Hence, we have
$90{}^\circ =90{}^\circ -x+\angle DAC\Rightarrow \angle DAC=x$
Hence, we have
$\angle ABD=\angle DAC$
Similarly, we can prove that $\angle ACD=\angle DAB$
Now in triangles ADB and CDA, we have
$\begin{aligned} & \angle ABD=\angle DAC\left( \operatorname{P}\text{roved above} \right) \\\ & \angle DAB=\angle ACD\left( \text{Proved above} \right) \\\ & \angle ADB=\angle ADC\left( \text{Each 90}{}^\circ \right) \\\ \end{aligned}$
Hence, we have
$\Delta ADB\sim \Delta CDA$(By A.A.A. similarity criterion)
Hence, we have
$\dfrac{AD}{CD}=\dfrac{BD}{AD}$(Because sides of similar triangles are proportional.
Cross-multiplying, we get
$A{{D}^{2}}=BD\times CD$

Note: [1] The first part of the result is a direct result of the theorem two triangles similar to the same triangle are similar to each other Both triangles ADB and CDA are similar to triangle CAB (Property used in the proof of Pythagoras theorem). Hence they are similar to each other.
[2] The second part of the result can be proved independently using Pythagoras theorem.
We have in triangle ADB $A{{D}^{2}}+D{{B}^{2}}=A{{B}^{2}}\text{ }\left( i \right)$ and in triangle A.D.C., we have
$A{{D}^{2}}+D{{C}^{2}}=A{{C}^{2}}\text{ }\left( ii \right)$
Adding equation (i) and equation (ii), we get
$2A{{D}^{2}}+D{{C}^{2}}+D{{B}^{2}}=A{{B}^{2}}+A{{C}^{2}}$
From triangle ABC, we have $A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}$
Hence we have
$2A{{D}^{2}}+D{{C}^{2}}+D{{B}^{2}}=A{{C}^{2}}$
Adding $2DC\times DB$ on both sides, we get
$2A{{D}^{2}}+D{{C}^{2}}+D{{B}^{2}}+2DC\times DB=A{{C}^{2}}+2DC\times DB$
Hence using the identity, ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab,$ we get
$\begin{aligned} & 2A{{D}^{2}}+{{\left( DB+DC \right)}^{2}}=A{{C}^{2}}+2DC\times DB \\\ & \Rightarrow 2A{{D}^{2}}+A{{C}^{2}}=A{{C}^{2}}+2DC\times DB \\\ & \Rightarrow 2A{{D}^{2}}=2DC\times DB \\\ & \Rightarrow A{{D}^{2}}=DC\times DB \\\ \end{aligned}$