Question

If a perpendicular distance of a point $P$ from the ${x \ axis}$ is $5 \ units$ and the foot of the perpendicular lies on the negative direction of the ${x \ axis}$. The point $P$ has

Answer 1

In the given question, it’s given that the perpendicular distance of a point $P$ from the ${x \ axis}$ has $5 \ units$. We need to find the coordinate of P in this question.Perpendicular distance is nothing but the shortest distance from the point to the line.

Complete answer: We know that the perpendicular distance of a point from the ${x \ axis}$ gives ${x \ axis}$ coordinate of that point .
.i.e). $x$ coordinate is always perpendicular to the ${y \ axis}$

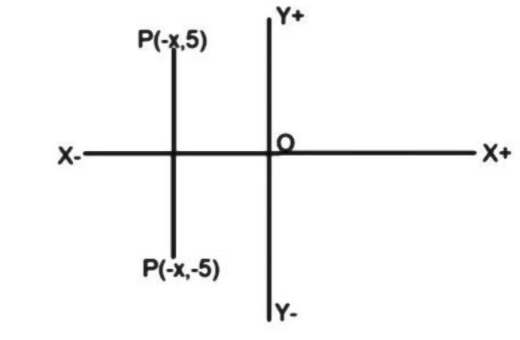
Here the foot of the perpendicular lies in the negative direction of ${ x \ axis}$, so the perpendicular distance can be measured in ll quadrant or lll quadrant.
From this we can conclude that the point $P$ has $y$ co-ordinate $= 5 \ or \ - 5$
The point $P$ has ordinate $= \ 5\ or\ - 5$
Final answer :
The point $P$ has ordinate $= \ 5\ or\ - 5$

Note:
The shortest distance of one point from the plane is called the perpendicular distance of that point. Basically there are two methods to calculate the perpendicular distance of a point . They are
-Vector method
-Cartesian method
We need to be careful that by mistake we might think the $\ y$ -coordinate is the perpendicular distance from the $y$ -axis but it is not, the $x$ -coordinate is the perpendicular distance from the $y$- axis. First we need to know that the horizontal axis is known as $x$ axis and the vertical axis is known as the $y$ axis.