Question

If a particle slides back and forth between two smooth planes as shown in the figure, then the correct statement is/are:

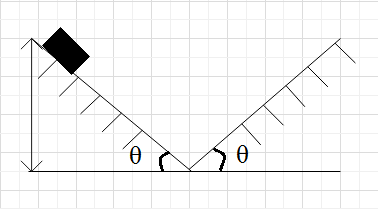
(A) The motion is oscillatory
(B) The motion is SHM
(C) If h is the initial height, then it’s period $T = \dfrac{4}{{\sin \theta }}\sqrt {\dfrac{{2h}}{g}}$
(D) If h is the initial height, then it’s period $T = \dfrac{2}{{\sin \theta }}\sqrt {\dfrac{{2h}}{g}}$

Answer 1

Hint
This question is typically based on the combined concepts of the force and the displacement. We need to find the acceleration of the body in terms of the acceleration due to gravity and then find the distance travelled by the body for the first half of its motion. Using these 2 values we can find the time period of the body.
In this solution we will be using the following formula,
$\Rightarrow F = ma$
Where $F$ is the force on the body on mass $m$, causing an acceleration $a$
$\Rightarrow s = ut + \dfrac{1}{2}a{t^2}$
where $s$ is the distance travelled,
$u$ is the initial velocity
and $t$ is the time.

Complete step by step answer
To solve this problem, let us first consider the following figure,

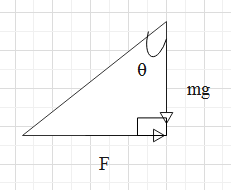
The force acts on the particle along the direction of the slide. The normal force, that is, $mg$ acts in the downward direction.
Therefore, we obtain an expression as the sine of an angle is the ratio of the perpendicular and hypotenuse of a triangle.
$\Rightarrow \sin \theta = \dfrac{F}{{mg}}$
So we can take the $g$ from the RHS to the LHS and write,
$\Rightarrow g\sin \theta = \dfrac{F}{m}$
Again we can express the above equation in terms of the acceleration as follows,
$\Rightarrow a = \dfrac{F}{m}$
So from the 2 equations we can relate the acceleration of the body to the acceleration due to gravity as,
$\Rightarrow g\sin \theta = a$
Therefore, from the above expression, we can see that the acceleration of the given particle is constant.
In the case of SHM, the acceleration will be proportional to the displacement, that is, $a \propto ( - x)$.
But, here, in the given case, the acceleration is constant, thus, option (B) is wrong.
Now let us consider the equation of motion for further solving of the problem.
So, using the second law of motion, we have,
$\Rightarrow s = ut + \dfrac{1}{2}a{t^2}$
The distance travelled by the particle can be found by the following diagram,

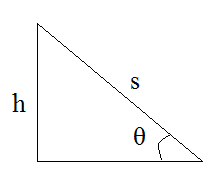
We can write from here,
$\Rightarrow \sin \theta = \dfrac{h}{s}$
Therefore, we can write the distance travelled as,
$\Rightarrow s = \dfrac{h}{{\sin \theta }}$
Now by substituting the values of the acceleration and the distance travelled by the particle in the equation of motion, we get,
$\Rightarrow \dfrac{h}{{\sin \theta }} = (0)t + \dfrac{1}{2}(g\sin \theta ){t^2}$
The initial velocity is considered to be 0 so the first term 0.
Therefore, we can rearrange the terms as,
$\Rightarrow {t^2} = \dfrac{{2h}}{{g{{\sin }^2}\theta }}$
So we can get the time by taking square root on both sides as,
$\Rightarrow t = \dfrac{1}{{\sin \theta }}\sqrt {\dfrac{{2h}}{g}}$
This much time is taken by the particle to reach the bottom from the height ‘h’.
The four times of this time is needed by the particle to get back to its original position.

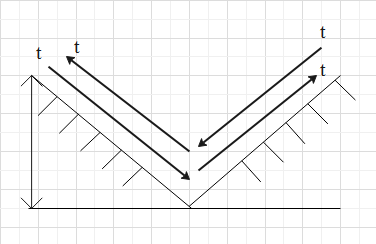
So, the time period of the particle is,
$\Rightarrow T = 4t$
This gives us,
$\Rightarrow T = \dfrac{4}{{\sin \theta }}\sqrt {\dfrac{{2h}}{g}}$
So, the motion of the particle is oscillatory with a time period of $\dfrac{4}{{\sin \theta }}\sqrt {\dfrac{{2h}}{g}}$, thus, the options (A) and (C) are correct.
Therefore, the options (A) and (C) are correct.
$\therefore$ If a particle slides back and forth between two smooth planes, the motion will be oscillatory with a time period of $\dfrac{4}{{\sin \theta }}\sqrt {\dfrac{{2h}}{g}}$.
Thus, the options (A) and (C) are correct.

Note
The simple harmonic motion is a kind of periodic motion where the restoring force is directly proportional to the magnitude of the displacement. Its direction is towards the equilibrium position of the body.