Question
Question: If a normal of slope m to the parabola \({{y}^{2}}=4ax\) touches the hyperbola \({{x}^{2}}-{{y}^{2}}...
If a normal of slope m to the parabola y2=4ax touches the hyperbola x2−y2=a2 , then:
(a) m6−4m4−3m2+1=0
(b) m6−4m4+3m2−1=0
(c) m6+4m4−3m2+1=0
(d) m6+4m4+3m2+1=0
Solution
Hint: The normal of slope m to the parabola y2=4ax is given by y=mx−2am−am3 while the tangent of slope m to the hyperbola a2x2−b2y2=1 is given by y=mx±a2m2−b2 . Also, the statement that the normal to the parabola touches the hyperbola indicates that the equation of normal of slope m to the parabola is the same as the equation of tangent of slope m to the given hyperbola, so equate the constants of both the equations to get the answer.
Complete step-by-step solution -
Let us start by drawing a representative diagram of the situation mentioned in the question.
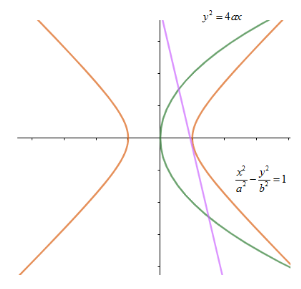
Now let us first find the equation of normal to the parabola. We know that the normal of slope m to the parabola y2=4ax is given by y=mx−2am−am3 .
Now as it is given that the normal to the parabola touches the hyperbola indicates that the equation of normal of slope m to the parabola is the same as the equation of tangent of slope m to the given hyperbola.
Also, we know that the tangent of slope m to the hyperbola a2x2−b2y2=1 is given by y=mx±a2m2−b2 . So, for the hyperbola a2x2−a2y2=1 , the tangent of slope m has equation:
y=mx±a2m2−a2
⇒y=mx±am2−1
Now as it is given that the normal to the parabola touches the hyperbola indicates that the equation of normal of slope m to the parabola is the same as the equation of tangent of slope m to the given hyperbola. So, we will equate the constant terms of the tangent of the hyperbola and the constant term of the normal to the parabola.
±am2−1=−2am−am3
Now we will square both sides of the equation. On doing so, we get
(±m2−1)2=(−2m−m3)2
⇒(m2−1)2=(2m+m3)2
For squaring RHS, we will use the formula (a+b)2=a2+b2+2ab.
m2−1=m6+4m2+4m4
⇒m6+4m4+4m2−m2+1=0
⇒m6+4m4+3m2+1=0
Therefore, the answer to the above question is option (d).
Note: If you don’t remember the formulas of normal and tangents of conics with a given slope you can use the method of application of derivatives for finding the equations. Also, if you are using the formulas be very careful about each and every sign, as one sign can change the whole result and the signs are very confusing too.
