Question

If $a\ne 0$ and the line $2bx+3cy+4d=0$ passes through the points of intersection of the parabola ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$, prove that ${{d}^{2}}+{{\left( 2b+3c \right)}^{2}}=0$.

Answer 1

Hint: We have to find the values of $x$ and $y$ to get the points of intersection of the two parabolas by rearranging the two equations ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$. Then, it can be substituted in the equation of the line.

Complete step-by-step answer:
Two parabolas ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$ are given in the question. A line that passes through the points of their intersection is given as $2bx+3cy+4d=0$. Let us consider the plot as below,

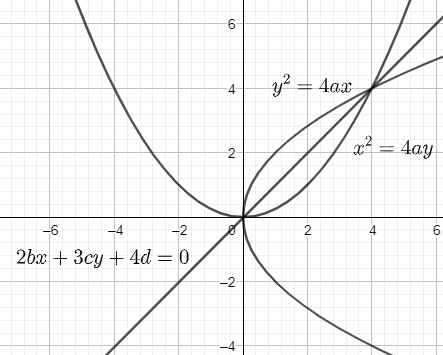
The first step is to find the points of intersection of the parabolas. Let us consider the two equations as below,
${{y}^{2}}=4ax\ldots \ldots \ldots \left( i \right)$
${{x}^{2}}=4ay\ldots \ldots \ldots \left( ii \right)$
From equation $\left( ii \right)$, we can substitute $y=\dfrac{{{x}^{2}}}{4a}$ in equation $\left( i \right)$. Therefore, we get
$\begin{aligned} & {{\left[ \dfrac{{{x}^{2}}}{4a} \right]}^{2}}=4ax \\\ & \dfrac{{{x}^{4}}}{16{{a}^{2}}}=4ax \\\ & \dfrac{{{x}^{4}}}{16{{a}^{2}}}-4ax=0 \\\ \end{aligned}$
Taking LCM, we get,

& \dfrac{{{x}^{4}}-64{{a}^{3}}x}{16{{a}^{2}}}=0 \\\ & {{x}^{4}}-64{{a}^{3}}x=0 \\\ \end{aligned}$$ Taking the common term $$x$$ outside, we get $$x\left( {{x}^{3}}-64{{a}^{3}} \right)=0$$ We can have the values of $$x$$ as, $$x=0$$ and $$\begin{aligned} & {{x}^{3}}-64{{a}^{3}}=0 \\\ & {{x}^{3}}=64{{a}^{3}} \\\ \end{aligned}$$ Taking the cube root, we get $$x=4a$$ Therefore, the values of $$x$$ are $$0$$ and $4a$. Substituting the value of $$x=0$$ in equation $\left( i \right)$, we can find the value of $$y$$ as, $\begin{aligned} & {{y}^{2}}=4a\times 0 \\\ & y=0 \\\ \end{aligned}$ Substituting the value of $$x=4a$$ in equation $\left( i \right)$, we can find the value of $$y$$ as, $\begin{aligned} & {{y}^{2}}=4a\times 4a \\\ & y=4a \\\ \end{aligned}$ Therefore, the values of $$y$$ are also obtained as $$0$$ and $4a$. So, the points of intersection of the parabolas $${{y}^{2}}=4ax$$ and $${{x}^{2}}=4ay$$ are $$\left( 0,0 \right)$$ and $$\left( 4a,4a \right)$$. Now, since it is given that the line $$2bx+3cy+4d=0$$ passes through the intersection points of the parabolas, we can substitute each of these points in the equation of the line. Substituting point $$\left( 0,0 \right)$$ first, we get $$\begin{aligned} & 2b\times 0+3c\times 0+4d=0 \\\ & d=0 \\\ \end{aligned}$$ Next, substituting point $$\left( 4a,4a \right)$$, we get $$\begin{aligned} & 2b\times 4a+3c\times 4a+4d=0 \\\ & 8ba+12ca+4d=0 \\\ \end{aligned}$$ Since we have the result $$d=0$$, we get, $8ba+12ca=0$ Taking out the common term $4a$, we get $$\begin{aligned} & 4a\left( 2b+3c \right)=0 \\\ & 2b+3c=0 \\\ & 2b=-3c \\\ \end{aligned}$$ As per the question, we have to prove that $${{d}^{2}}+{{\left( 2b+3c \right)}^{2}}=0$$. The value of $$d$$ is $$0$$ and also we have $2b=-3c$. Considering the $$LHS$$ of the expression to be proved, $$\begin{aligned} & {{d}^{2}}+{{\left( 2b+3c \right)}^{2}} \\\ & {{0}^{2}}+{{\left( 2b-2b \right)}^{2}} \\\ & 0+0 \\\ & 0=RHS \\\ \end{aligned}$$ Since $$LHS$$ is equal to $$RHS$$, it is proved. Note: The points of intersection of two parabolas can be found by looking at the equations given in the question, i.e. $${{y}^{2}}=4ax$$ and $${{x}^{2}}=4ay$$. When we substitute $$x=0$$ in both equations, we get$$y=0$$. Also, the term $4a$ is common to both and the equations have a square term on the $$LHS$$. So, that is possible only when we have $$x=y=4a$$.