Question

If $a = \max\{(x + 2)^2 + (y - 3)^2\}$ and $b = \min\{(x+2)^2 +(y-3)^2\}$ where $x, y$ satisfying $x^2 + y^2 + 8x – 10y – 40 = 0$, then :

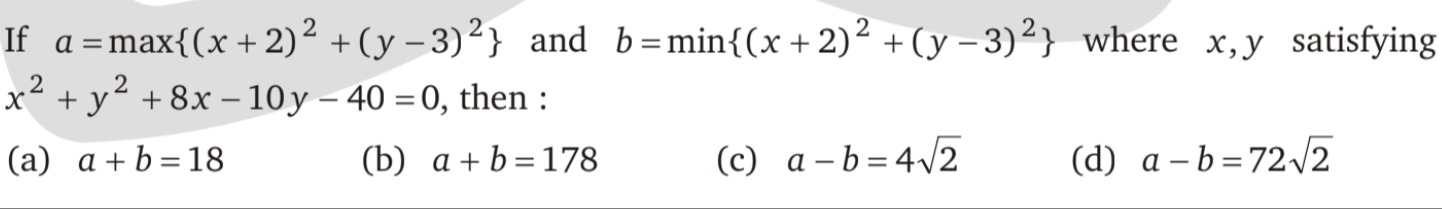
• A. $a + b = 18$
• B. $a+b=178$
• C. $a-b = 4\sqrt{2}$
• D. $a-b=72\sqrt{2}$

Answer 1

Answer: (B), (D)

b, d

Answer 2

The problem asks us to find the maximum and minimum values of the expression $(x + 2)^2 + (y - 3)^2$ subject to the constraint $x^2 + y^2 + 8x – 10y – 40 = 0$. Let $P = (x + 2)^2 + (y - 3)^2$.

1. Analyze the Constraint Equation: The constraint $x^2 + y^2 + 8x – 10y – 40 = 0$ represents a circle. To find its center and radius, we complete the square: $(x^2 + 8x) + (y^2 - 10y) = 40$ $(x^2 + 8x + 16) + (y^2 - 10y + 25) = 40 + 16 + 25$ $(x + 4)^2 + (y - 5)^2 = 81$ This is the equation of a circle with center $C_1 = (-4, 5)$ and radius $R_1 = \sqrt{81} = 9$.

2. Interpret the Expression to be Optimized: The expression $P = (x + 2)^2 + (y - 3)^2$ represents the square of the distance between a point $(x, y)$ on the circle and a fixed point $C_2 = (-2, 3)$. Let $D$ be the distance between $(x, y)$ and $C_2$. Then $P = D^2$. We need to find the maximum and minimum values of $D^2$.

3. Calculate the Distance Between the Centers: First, find the distance $d$ between the center of the circle $C_1 = (-4, 5)$ and the fixed point $C_2 = (-2, 3)$: $d = \sqrt{(-2 - (-4))^2 + (3 - 5)^2}$ $d = \sqrt{(2)^2 + (-2)^2}$ $d = \sqrt{4 + 4}$ $d = \sqrt{8} = 2\sqrt{2}$.

4. Determine Maximum and Minimum Distances: Compare the distance $d$ with the radius $R_1$: $d = 2\sqrt{2} \approx 2 \times 1.414 = 2.828$ $R_1 = 9$ Since $d < R_1$, the point $C_2$ lies inside the circle.

   For a point inside a circle, the minimum distance from the point to any point on the circle is $R_1 - d$. The maximum distance from the point to any point on the circle is $R_1 + d$.

   So, the minimum distance $D_{min} = R_1 - d = 9 - 2\sqrt{2}$. The maximum distance $D_{max} = R_1 + d = 9 + 2\sqrt{2}$.

5. Calculate $a$ and $b$: $a = \max\{(x + 2)^2 + (y - 3)^2\} = (D_{max})^2$ $a = (9 + 2\sqrt{2})^2 = 9^2 + (2\sqrt{2})^2 + 2 \cdot 9 \cdot 2\sqrt{2}$ $a = 81 + (4 \cdot 2) + 36\sqrt{2}$ $a = 81 + 8 + 36\sqrt{2}$ $a = 89 + 36\sqrt{2}$.

   $b = \min\{(x + 2)^2 + (y - 3)^2\} = (D_{min})^2$ $b = (9 - 2\sqrt{2})^2 = 9^2 + (2\sqrt{2})^2 - 2 \cdot 9 \cdot 2\sqrt{2}$ $b = 81 + 8 - 36\sqrt{2}$ $b = 89 - 36\sqrt{2}$.

6. Check the Options: (a) $a + b = 18$ $a + b = (89 + 36\sqrt{2}) + (89 - 36\sqrt{2}) = 89 + 89 = 178$. So, (a) is incorrect.

   (b) $a + b = 178$ This matches our calculation. So, (b) is correct.

   (c) $a - b = 4\sqrt{2}$ $a - b = (89 + 36\sqrt{2}) - (89 - 36\sqrt{2}) = 89 + 36\sqrt{2} - 89 + 36\sqrt{2} = 72\sqrt{2}$. So, (c) is incorrect.

   (d) $a - b = 72\sqrt{2}$ This matches our calculation. So, (d) is correct.

Both options (b) and (d) are correct.