Question
Question: If a man of height \(6\)ft walks at a uniform speed of \(9\)ft/sec from a lamp of height \(15\)ft th...
If a man of height 6ft walks at a uniform speed of 9ft/sec from a lamp of height 15ft then the length of his shadow is increasing at the rate of
(A)6ft/sec
(B)12ft/sec
(C)10ft/sec
(D)15ft/sec
Solution
First of all, we have to find the length of shadow (sayx) and then apply following formula to find the rate of increase of length of shadow, i.e., speed of shadow (vs):
vs=dtdx
Complete step-by-step answer:
Given, height of a man= 6ft
Speed of man= 9ft/sec
Height of lamp= 15ft
We have to calculate the rate of increase of length of shadow, i.e., speed of shadow (vs).
After ‘t’sec, the man would move a distance of 9t ft away from the lamp. Let the shadow move a distance of xft in ‘t’sec.
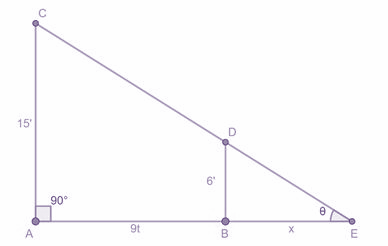
Consider ΔAEC and ΔBED;
∠AEC=∠BED=θ (common angle)
∠EAC=∠EBD=90∘
∴ ΔAEC∼ΔBED (By AA criteria of similarity of triangles)
We know that if two triangles are similar then their corresponding sides are in the same ratio.
∴BDAC=BEAE
On substituting the values, we get-
615=x9t+x
On simplifying it, we get-
⇒15x=54t+6x
⇒15x−6x=54t
⇒9x=54t
⇒x=954t
⇒x=6t ….. (1)
As we know that the derivative of displacement(x) with respect to time (t) gives us the velocity.
Therefore, velocity of shadow, vs=dtdx
⇒vs=dtd(6t)
⇒vs=6 ft/sec
Therefore, the length of shadow is increasing at the rate of 6ft/sec.
So, option (A) is the correct answer.
Note: Here we use AA (Angle-Angle) criteria of similarity which states that if two corresponding angles of two triangles are equal, then two triangles are similar. Also, similar triangles have a property that their corresponding sides are in the same ratio.
