Question

If a line segment $AM =$ $a$ moves in the plane $XOY$ remaining parallel to $OX$ so that the left end point $A$ slides along the circle ${x^2} + {y^2} = {a^2}$ , the locus of $M$ is
A) ${x^2} + {y^2} = 4{a^2}$
B) ${x^2} + {y^2} = 2ax$
C) ${x^2} + {y^2} = 2ay$
D) ${x^2} + {y^2} - 2ax - 2ay = 0$

Answer 1

Here, we have to find the locus of M. The set of all points which form geometrical shapes such as a line, a line segment, circle, a curve, etc., and whose location satisfies the conditions is the locus.

Formula Used:
We will use the following formulas:

1. Equation of the circle is of the form ${x^2} + {y^2} = {a^2}$ where $x$ is the distance from the origin along the $x$ axis, $y$ is the distance from the origin along the $y$ axis and $a$ is the radius of the circle.
2. The square of the difference of two numbers is given by the algebraic identity ${(a - b)^2} = {a^2} + {b^2} - 2ab$ where $a$ and $b$ are two numbers.

Complete step by step solution:
We are given a line segment in the plane $XOY$ which is parallel to $OX$. The line segment $AM =$ $a$lies in the plane $XOY$. The point $A$ slides along the circle ${x^2} + {y^2} = {a^2}$. Let the coordinates of $A$ be $(x,y)$ and $M$ be $(\alpha ,\beta )$ .

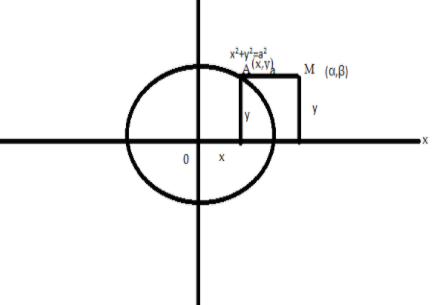
Since $AM$ is parallel to $OX$
The points at $M$ be $OM = OX + XM$
Here $OM = \alpha$; $OX = x$ ; $XM = a$ because $\left[ {XM = AM} \right]$.
So, we have $\alpha = x + a$ and $\beta = y$
Now, we have $x = \alpha - a;y = \beta$
So, the coordinates of $M$ are $(\alpha - a,\beta )$
We know that the point $A$ slides along the circle ${x^2} + {y^2} = {a^2}$
Since $AM$ is a line segment, the point $M$also slides along the circle.
Substituting the coordinates of $M$ in the equation of the circle, we have
$\Rightarrow {(\alpha - a)^2} + {\beta ^2} = {a^2}$
The square of the difference of two numbers is given by the algebraic identity ${(a - b)^2} = {a^2} + {b^2} - 2ab$ where $a$ and $b$ are two numbers.
Now, by using the algebraic identity, we get
$\Rightarrow ({\alpha ^2} + {a^2} - 2a\alpha ) + {\beta ^2} = {a^2}$
Simplifying the equation, we have
$\Rightarrow {\alpha ^2} - 2a\alpha + {\beta ^2} = 0$
Rewriting the equation, we have
$\Rightarrow {\alpha ^2} + {\beta ^2} = 2a\alpha$
Since $(\alpha ,\beta )$ are the coordinates of $M$ , we have
$\Rightarrow {x^2} + {y^2} = 2ax$

Therefore, the locus of $M$ is ${x^2} + {y^2} = 2ax$

Note:
We know that a locus is a set of all the points whose position is defined by certain conditions. We have to find the location of $M$. We have important conditions to find out the locus. The locus at the fixed distance $d$ from the point $p$ is considered as a circle with $p$ as its center and $d$ as its diameter. Every point which satisfies the given geometrical condition lies on the focus. A point which does not satisfy the given geometrical condition cannot lie on the focus.