Question

If a line makes angles of ${{60}^{\circ }}$ and ${{45}^{\circ }}$ with the positive directions of the x-axis and y-axis respectively. Then find the acute angle between the line and the z-axis.
A. ${{60}^{\circ }}$
B. ${{45}^{\circ }}$
C. ${{75}^{\circ }}$
D. ${{15}^{\circ }}$

Answer 1

We need to find the angles and their cosines for the line with the axes. We have the theorem that the sum of the squares of the cosines are always 1. We apply the formula to find the equation. We solve the problem and find the solution of $\cos \lambda =\dfrac{1}{2}$. The angle being acute, we find the value of $\lambda$ for ${{0}^{\circ }}<\lambda <{{90}^{\circ }}$.

Complete step-by-step answer:
We have been given that a line makes angles of ${{60}^{\circ }}$ and ${{45}^{\circ }}$ with the positive directions of the x-axis and y-axis respectively.

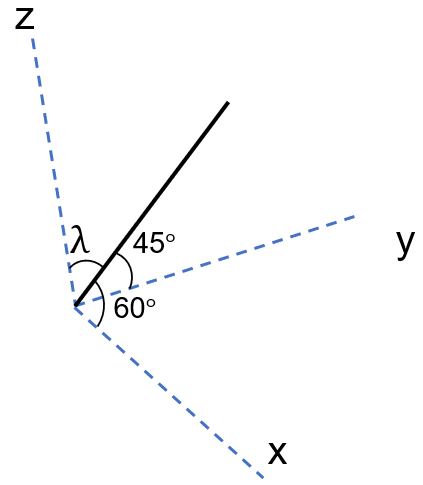
For the line the angles with the x-axis and y-axis are $\alpha ={{60}^{\circ }}$ and $\beta ={{45}^{\circ }}$ respectively. Let’s assume that the acute angle between the line and the z-axis is $\lambda$.
We find the cosines of the line by taking the trigonometric ratio of $\cos$ on every angle for the axes, assuming them as l, m, n.
So, $l=\cos \alpha =\cos {{60}^{\circ }}=\dfrac{1}{2}$ and $m=\cos \beta =\cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$. We also have $n=\cos \lambda$.
We know that the sum of the squares of the cosines are always 1.
So, ${{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\lambda =1$. We place the values to get
$\begin{aligned} & {{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\lambda =1 \\\ & \Rightarrow {{\left( \dfrac{1}{2} \right)}^{2}}+{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}+{{\cos }^{2}}\lambda =1 \\\ \end{aligned}$
Now we solve the equation and try to find the value of ${{\cos }^{2}}\lambda$.

& {{\left( \dfrac{1}{2} \right)}^{2}}+{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}+{{\cos }^{2}}\lambda =1 \\\ & \Rightarrow \dfrac{1}{4}+\dfrac{1}{2}+{{\cos }^{2}}\lambda =1 \\\ & \Rightarrow {{\cos }^{2}}\lambda =1-\dfrac{3}{4}=\dfrac{1}{4} \\\ \end{aligned}$$ As the angles $\lambda $ is acute which means ${{0}^{\circ }}<\lambda <{{90}^{\circ }}$, the value of $\cos \lambda $ will be positive. So, ${{\cos }^{2}}\lambda =\dfrac{1}{4}\Rightarrow \cos \lambda =\dfrac{1}{2}$. The value of $\lambda $ will be $\lambda ={{60}^{\circ }}$ as $\cos \lambda =\dfrac{1}{2}$. **So, the correct answer is “Option A”.** **Note:** We need to remember that the value of $\cos \lambda $ will remain in $0<\cos \lambda <1$ for ${{0}^{\circ }}<\lambda <{{90}^{\circ }}$. The angle between the line and the axis can be obtuse also as we are dealing with 3-d geometry.