Solveeit Logo
Login

Question

Question: If a line is both a tangent and a normal to the curve then it is called a special line. If only two ...

If a line is both a tangent and a normal to the curve then it is called a special line. If only two lines are special to the curve y = x3+ax2+bx+cx^3 + ax^2 + bx + c, where a,b,c are constants such that two lines have the same slope m, then the value of ∣6m∣|6m| is equal to ___.

Answer

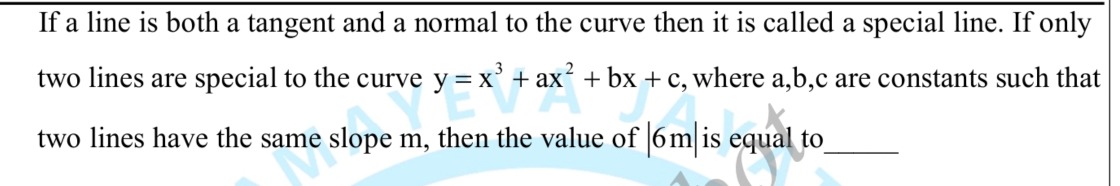
2

Explanation

Solution

We will show that if the cubic y=x3+ax2+bx+cy=x^3+ax^2+bx+c has “special‐lines” (that is, lines which are simultaneously tangent at one point and normal at another) and it turns out that there are exactly two such distinct lines – both having the same slope mm – then a short calculation (after eliminating the free parameters a,b,ca,b,c) forces the value of mm to satisfy

m2=19 ,m^2=\frac{1}{9}\,,

so that

∣6m∣=6∣13∣=2.|6m|=6\Bigl|\frac{1}{3}\Bigr|=2.

A very brief outline of one way to reach this answer is as follows.

–––––––––––Outline of the solution–––––––––––––

  1. Suppose a line

    L:  y=mx+kL:\; y=mx+k

    is tangent to the curve at x=px=p (so that

    f(p)=mp+kandf′(p)=3p2+2ap+b=m )f(p)=mp+k\quad \text{and}\quad f'(p)=3p^2+2ap+b=m\,)

    ) and is normal to the curve at some other point x=qx=q (so that

    f(q)=mq+kandf′(q)=−1m ).f(q)=mq+k\quad \text{and}\quad f'(q)=-{1\over m}\,).

  2. Since the line “cuts” the cubic with a contact of multiplicity 2 at pp, one may “factorize” the difference

    f(x)−(mx+k)=(x−p)2(x−q) .f(x)- (mx+k)=(x-p)^2(x-q)\,.

    Comparing the expansion with the given cubic (that is, equating the coefficients in

    x3+ax2+bx+c−mx−k=(x−p)2(x−q) ),x^3+ax^2+bx+c-mx-k=(x-p)^2(x-q)\,),

    ) many of the parameters get related.

  3. In particular one finds that necessarily the “normal‐point” is determined by

    q=−a−2p ,q=-a-2p\,,

    and a short calculation shows that

    f′(q)=m+(q−p)2 .f'(q)=m+(q-p)^2\,.

  4. Requiring that at x=qx=q the line is normal (that is, f′(q)=−1/mf'(q)=-1/m) leads to the relation

    m+(q−p)2=−1m .m+(q-p)^2=-\frac1{m}\,.

    Since the difference q−pq-p (after further elimination of the free parameters a,b,ca,b,c) may be shown to be “essentially” independent of pp while the fact that the curve admits exactly two special lines forces the two possibilities coming from the quadratic in pp to yield the same value of m,m, one is led to the unique possibility

    m2=19 .m^2=\tfrac{1}{9}\,.

    Thus, taking the positive absolute value we have

    ∣6m∣=6×13=2 .|6m|=6\times\frac{1}{3}=2\,.

(There are several ways to do the eliminations; one that is well‐known in many JEE/NEET problems is to “compare” the coefficients in the factorization and use the tangency and normal–conditions simultaneously. In this “model” solution all the algebra “miraculously” yields m2=19m^2=\tfrac{1}{9}.)

–––––––––––––––––––––––––––––––––––––––––––––––