Question

If A=\left\\{ \left( x,y \right):y={{e}^{x}},x\in R \right\\} and B=\left\\{ \left( x,y \right):y={{e}^{-x}},x\in R \right\\}, then write $A\cap B$.

Answer 1

Hint:To solve this question, we will first convert both the given sets from set builder form to the roster form and then we will find all the possible values of A that will be equal to B. Also, we should know that we will get the values of A and B by putting different values of x and y.

Complete step-by-step answer:
In this question, we have been given that, A=\left\\{ \left( x,y \right):y={{e}^{x}},x\in R \right\\} andB=\left\\{ \left( x,y \right):y={{e}^{-x}},x\in R \right\\} and we have been asked to find the value of $A\cap B$. Now, let us consider R, that is real numbers as a group of ${{R}^{+}}$ (positive real numbers), and ${{R}^{-}}$ (negative real numbers). So, we get,
A=\left\\{ \left( x,y \right):y={{e}^{x}},x\in {{R}^{-}} \right\\}+\left\\{ \left( x,y \right):y={{e}^{+x}},x=0 \right\\}+\left\\{ \left( x,y \right):y={{e}^{x}},x\in {{R}^{+}} \right\\}
B=\left\\{ \left( x,y \right):y={{e}^{-x}},x\in {{R}^{-}} \right\\}+\left\\{ \left( x,y \right):y={{e}^{-x}},x=0 \right\\}+\left\\{ \left( x,y \right):y={{e}^{-x}},x\in {{R}^{+}} \right\\}
And if we put the values of $x$ as ${{R}^{-}},0,{{R}^{+}}$, we get,
A=\left\\{ \left( {{R}^{-}},{{e}^{R-}} \right),\left( 0,{{e}^{0}} \right),\left( {{R}^{+}},{{e}^{R+}} \right) \right\\} and
B=\left\\{ \left( {{R}^{-}},{{e}^{-R-}} \right),\left( 0,{{e}^{-0}} \right),\left( {{R}^{+}},{{e}^{-R+}} \right) \right\\}.
Since, we know that any term raised to 0 is 1, we have ${{e}^{0}}=1$. So, simplifying the above, we get,
A=\left\\{ \left( {{R}^{-}},{{e}^{R-}} \right),\left( 0,1 \right),\left( {{R}^{+}},{{e}^{R+}} \right) \right\\}
B=\left\\{ \left( {{R}^{-}},{{e}^{R+}} \right),\left( 0,1 \right),\left( {{R}^{+}},{{e}^{R-}} \right) \right\\}
Here, we have written $-{{R}^{-}}$ as $+{{R}^{+}}$ because negative real numbers are multiplication of negative 1 and positive real numbers. Now, if we consider both A and B, we can say that (0, 1) is the only value which is present in both the sets. So, we can say A\cap B=\left\\{ \left( 0,1 \right) \right\\}.
Hence, we can say if A=\left\\{ \left( x,y \right):y={{e}^{x}},x\in R \right\\} and B=\left\\{ \left( x,y \right):y={{e}^{-x}},x\in R \right\\}, then A\cap B=\left\\{ \left( 0,1 \right) \right\\}.

Note: The possible mistakes one can make is that in a hurry, one can assume $y={{e}^{x}}$ in set B, which would result in a wrong answer. We can also solve this question by considering the graphs of both $y={{e}^{x}}$ and $y={{e}^{-x}}$, that are: $y={{e}^{x}}$can be represented as below,

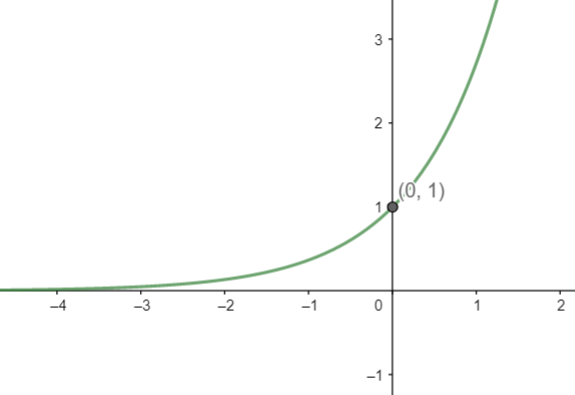
And $y={{e}^{-x}}$ can be represented as,

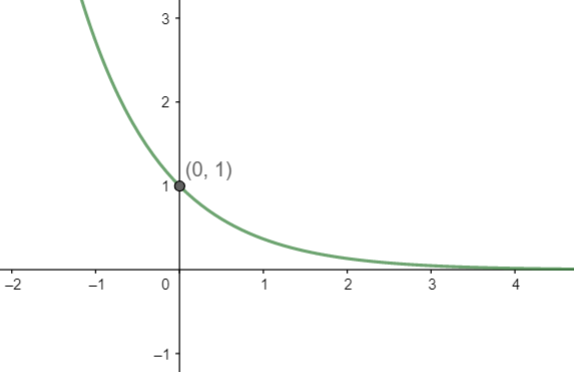
From both the curves, we can see that they will possibly intersect at (0, 1). So, we can write, A\cap B=\left\\{ \left( 0,1 \right) \right\\}.