Question

If A=\left\\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}=25 \right\\} and B=\left\\{ \left( x,y \right):{{x}^{2}}+9{{y}^{2}}=144 \right\\}, then $A\bigcap B$ contains
[a] one point
[b] three points
[c] two points
[d] four points.

Answer 1

Hint: Assume (x,y) is in both sets A and B. Hence using the definitions of sets A and B form two equations in x and y. Solve for x and y. The number of solutions of the system is the number of points in $A\bigcap B$. Hence find the number of points in $A\bigcap B$. Alternatively, plot the two equations on a graph paper. The number of points of intersection of both curves gives the number of points in the intersection of sets A and B.

Complete step-by-step solution -

Let (x,y) be an element in both A and B.
Since (x,y) is in A, we have
${{x}^{2}}+{{y}^{2}}=25\text{ (i)}$
Also, since (x,y) is in B, we have
${{x}^{2}}+9{{y}^{2}}=144\text{ (ii)}$
Subtracting equation (i) from equation (ii), we get
$\begin{aligned} & 9{{y}^{2}}-{{y}^{2}}=144-25 \\\ & \Rightarrow 8{{y}^{2}}=119 \\\ \end{aligned}$
Dividing both sides by 8, we get
${{y}^{2}}=\dfrac{119}{8}$
Subtracting $\dfrac{119}{8}$ from both sides, we get
${{y}^{2}}-\dfrac{119}{8}=0$
Writing the above expression in ${{a}^{2}}-{{b}^{2}}$ form, we get
${{y}^{2}}-{{\left( \sqrt{\dfrac{119}{8}} \right)}^{2}}=0$
We know that $\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)$
Using the above formula, we get
$\left( y+\sqrt{\dfrac{119}{8}} \right)\left( y-\sqrt{\dfrac{119}{8}} \right)=0$
Using zero product property, we have
$y+\sqrt{\dfrac{119}{8}}=0$ or $y-\sqrt{\dfrac{119}{8}}=0$
Hence $y=-\sqrt{\dfrac{119}{8}}$ or $y=\sqrt{\dfrac{119}{8}}$.
Also. We have
${{x}^{2}}+{{y}^{2}}=25$
Substituting the value of ${{y}^{2}}$, we get
${{x}^{2}}+\dfrac{119}{8}=25$
Subtracting $\dfrac{119}{8}$ from both sides, we get
${{x}^{2}}=25-\dfrac{119}{8}=\dfrac{200-119}{8}=\dfrac{81}{8}$
Subtracting $\dfrac{81}{8}$ from both sides, we get
${{x}^{2}}-\dfrac{81}{8}=0$
Writing the above expression in ${{a}^{2}}-{{b}^{2}}$ form, we get
${{x}^{2}}-{{\left( \sqrt{\dfrac{81}{8}} \right)}^{2}}=0$
We know that $\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)$
Using the above formula, we get
$\left( x+\sqrt{\dfrac{81}{8}} \right)\left( x-\sqrt{\dfrac{81}{8}} \right)=0$
Using zero product property, we have
$x+\sqrt{\dfrac{81}{8}}=0$ or $x-\sqrt{\dfrac{81}{8}}=0$
Hence $x=-\sqrt{\dfrac{81}{8}}$ or $x=\sqrt{\dfrac{81}{8}}$.
Hence the solutions are $\left( \sqrt{\dfrac{81}{8}},\sqrt{\dfrac{119}{8}} \right),\left( -\sqrt{\dfrac{81}{8}},\sqrt{\dfrac{119}{8}} \right),\left( \sqrt{\dfrac{81}{8}},-\sqrt{\dfrac{119}{8}} \right)$ and $\left( -\sqrt{\dfrac{81}{8}},-\sqrt{\dfrac{119}{8}} \right)$.
Hence there are four points in $A\bigcap B$
Hence option [d] is correct.

Note: Alternatively, we have
${{x}^{2}}+{{y}^{2}}=25$ is an equation of a circle with centre at (0,0) and radius = 5
And ${{x}^{2}}+9{{y}^{2}}=144$ is an equation of an ellipse with centre at (0,0), major axis length as 24 and minor axis length as 8. The major axis is along the x-axis, and the minor axis is along the y-axis.
Keeping all these points in mind, we plot the curves, as shown below.

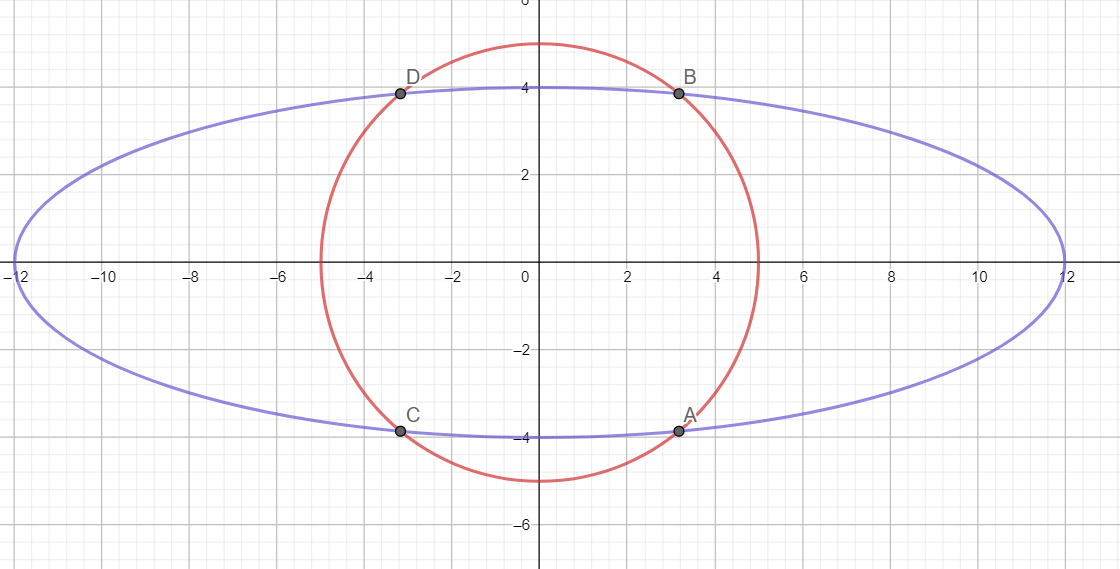
As is evident from the graph, there are four points of intersection. Hence the cardinality of $A\bigcap B$ is 4.