Solveeit Logo
Login

Question

Question: If \(A\left( -5,7 \right),B\left( -4,5 \right),C\left( -1,6 \right)\) and \(D\left( 4,5 \right)\) ar...

If A(−5,7),B(−4,5),C(−1,6)A\left( -5,7 \right),B\left( -4,5 \right),C\left( -1,6 \right) and D(4,5)D\left( 4,5 \right) are the vertices of a quadrilateral, then find its area.

Explanation

Solution

Divide the quadrilateral ABDC into two triangles ABC and BCD. Find the areas of the triangle ABC and BCD and hence find the area of the quadrilateral ABDC.
Use the property that if A≡(x1,y1),B≡(x2,y2)A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right) and C≡(x3,y3)C\equiv \left( {{x}_{3}},{{y}_{3}} \right) then the area of the triangle ABC is given by 12∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|.

Complete step-by-step answer:

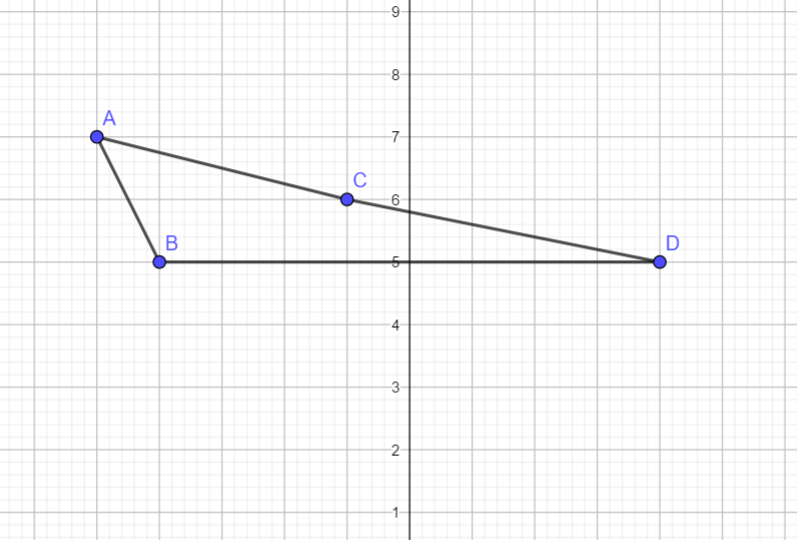
(Note that although ADC appears to be a straight line, it is not actually a straight line. This can be verified by finding the distances AC, CD and AD using distance formula and checking that AD≠AC+CDAD\ne AC+CD)
We have by distance formula, AC=(−5+4)2+(7−5)2=1+4=5AC=\sqrt{{{\left( -5+4 \right)}^{2}}+{{\left( 7-5 \right)}^{2}}}=\sqrt{1+4}=\sqrt{5}
Similarly by distance formula, we have AD=(−5+1)2+(7−6)2=16+1=17AD=\sqrt{{{\left( -5+1 \right)}^{2}}+{{\left( 7-6 \right)}^{2}}}=\sqrt{16+1}=\sqrt{17} and CD=(−4+1)2+(5−6)2=9+1=10CD=\sqrt{{{\left( -4+1 \right)}^{2}}+{{\left( 5-6 \right)}^{2}}}=\sqrt{9+1}=\sqrt{10}. Clearly, we have AC≠CD+ADAC\ne CD+AD. Hence, A,C and D are not collinear.
Finding the area of triangle ABC:
We know that if A≡(x1,y1),B≡(x2,y2)A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right) and C≡(x3,y3)C\equiv \left( {{x}_{3}},{{y}_{3}} \right) then the area of the triangle ABC is given by 12∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|.
We have x1=−5,x2=−4,x3=−1,y1=7,y2=5{{x}_{1}}=-5,{{x}_{2}}=-4,{{x}_{3}}=-1,{{y}_{1}}=7,{{y}_{2}}=5 and y3=6{{y}_{3}}=6
Hence the area of triangle ABC =12∣−5(5−6)−4(6−7)−1(7−5)∣=12∣5+4−2∣=72=3.5=\dfrac{1}{2}\left| -5\left( 5-6 \right)-4\left( 6-7 \right)-1\left( 7-5 \right) \right|=\dfrac{1}{2}\left| 5+4-2 \right|=\dfrac{7}{2}=3.5 square units.
Finding the area of the triangle BCD:
We know that if A≡(x1,y1),B≡(x2,y2)A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right) and C≡(x3,y3)C\equiv \left( {{x}_{3}},{{y}_{3}} \right) then the area of the triangle ABC is given by 12∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|.
We have x1=−4,x2=−1,x3=4,y1=5,y2=6{{x}_{1}}=-4,{{x}_{2}}=-1,{{x}_{3}}=4,{{y}_{1}}=5,{{y}_{2}}=6 and y3=5{{y}_{3}}=5
Hence the area of the triangle BCD =12∣−4(6−5)−1(5−5)+4(5−6)∣=12∣−4−0−4∣=4=\dfrac{1}{2}\left| -4\left( 6-5 \right)-1\left( 5-5 \right)+4\left( 5-6 \right) \right|=\dfrac{1}{2}\left| -4-0-4 \right|=4 square units
Hence the area of the quadrilateral ABDC = 4+3.5 = 7.5 square units.

Note: Alternative solution: Best Method.
If A≡(x1,y1),B≡(x2,y2),C≡(x3,y3)A\equiv \left( {{x}_{1}},{{y}_{1}} \right),B\equiv \left( {{x}_{2}},{{y}_{2}} \right),C\equiv \left( {{x}_{3}},{{y}_{3}} \right) and D≡(x4,y4)D\equiv \left( {{x}_{4}},{{y}_{4}} \right) are the vertices of a quadrilateral ABCD, then the area of the quadrilateral is given by
12∣x1−x3y1−y3 x2−x4y2−y4 ∣\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}}-{{x}_{3}} & {{y}_{1}}-{{y}_{3}} \\\ {{x}_{2}}-{{x}_{4}} & {{y}_{2}}-{{y}_{4}} \\\ \end{matrix} \right|
Here we have x1=−5,x2=−4,x3=4,x4=−1,y1=7,y2=5,y3=5{{x}_{1}}=-5,{{x}_{2}}=-4,{{x}_{3}}=4,{{x}_{4}}=-1,{{y}_{1}}=7,{{y}_{2}}=5,{{y}_{3}}=5 and y4=6.{{y}_{4}}=6.
Hence the area of the quadrilateral ABDC is given by 12∣−5−47−5 −4+15−6 ∣=12∣−92 −3−1 ∣=12(9+6)=152=7.5\dfrac{1}{2}\left| \begin{matrix} -5-4 & 7-5 \\\ -4+1 & 5-6 \\\ \end{matrix} \right|=\dfrac{1}{2}\left| \begin{matrix} -9 & 2 \\\ -3 & -1 \\\ \end{matrix} \right|=\dfrac{1}{2}\left( 9+6 \right)=\dfrac{15}{2}=7.5 square units, which is same as obtained above.