Solveeit Logo
Login

Question

Question: If \(A=\left\\{ 3,6,9,12,15,18,21 \right\\}\),\(B=\left\\{ 4,8,12,16,20 \right\\}\), \(C=\left\\{ 2,...

If A=\left\\{ 3,6,9,12,15,18,21 \right\\},B=\left\\{ 4,8,12,16,20 \right\\}, C=\left\\{ 2,4,6,8,10,12,14,16 \right\\} and D=\left\\{ 5,10,15,20 \right\\}; find
(i)A−B (ii)A−C (iii)A−D (iv)B−A (v)C−A (vi)D−A (vii)B−C (viii)B−D (ix)C−B (x)D−B (xi)C−D (xii)D−C \begin{aligned} & (i)A-B \\\ & (ii)A-C \\\ & (iii)A-D \\\ & (iv)B-A \\\ & (v)C-A \\\ & (vi)D-A \\\ & (vii)B-C \\\ & (viii)B-D \\\ & (ix)C-B \\\ & (x)D-B \\\ & (xi)C-D \\\ & (xii)D-C \\\ \end{aligned}

Explanation

Solution

In this question we have to find the difference between two sets. Subtraction of sets is found by removing the common elements of another set. We will use this concept to get the desired answer.

Complete step by step solution:
We have been given sets A=\left\\{ 3,6,9,12,15,18,21 \right\\},B=\left\\{ 4,8,12,16,20 \right\\}, C=\left\\{ 2,4,6,8,10,12,14,16 \right\\} and D=\left\\{ 5,10,15,20 \right\\}.
We have to find the difference between sets.
Now, we know that if we have two sets as A and B and we have to find the difference between sets as A−BA-B then we will remove the common element of set B from set A.
So by applying the above concept we will find the differences between sets.
Let us start solving the subparts of the given question. Then we will get
(i)A−B(i)A-B
Now, we have A=\left\\{ 3,6,9,12,15,18,21 \right\\},B=\left\\{ 4,8,12,16,20 \right\\}
Now, the removing the elements of set B from set A we will get
\Rightarrow A-B=\left\\{ 3,6,9,15,18,21 \right\\}
Hence above is the required answer.
(ii)A−C(ii)A-C
Now, we have A=\left\\{ 3,6,9,12,15,18,21 \right\\},C=\left\\{ 2,4,6,8,10,12,14,16 \right\\}
Now, the removing the elements of set C from set A we will get
\Rightarrow A-C=\left\\{ 3,9,15,18,21 \right\\}
Hence above is the required answer.
(iii)A−D(iii)A-D
Now, we have A=\left\\{ 3,6,9,12,15,18,21 \right\\},D=\left\\{ 5,10,15,20 \right\\}
Now, the removing the elements of set D from set A we will get
\Rightarrow A-D=\left\\{ 3,6,9,12,18,21 \right\\}
Hence above is the required answer.
(iv)B−A(iv)B-A
Now, we have A=\left\\{ 3,6,9,12,15,18,21 \right\\},B=\left\\{ 4,8,12,16,20 \right\\}
Now, the removing the elements of set A from set B we will get
\Rightarrow B-A=\left\\{ 4,8,16,20 \right\\}
Hence above is the required answer.
(v)C−A(v)C-A
Now, we have A=\left\\{ 3,6,9,12,15,18,21 \right\\},C=\left\\{ 2,4,6,8,10,12,14,16 \right\\}
Now, the removing the elements of set A from set C we will get
\Rightarrow C-A=\left\\{ 2,4,8,10,14,16 \right\\}
Hence above is the required answer.
(vi)D−A(vi)D-A
Now, we have A=\left\\{ 3,6,9,12,15,18,21 \right\\},D=\left\\{ 5,10,15,20 \right\\}
Now, the removing the elements of set A from set D we will get
\Rightarrow D-A=\left\\{ 5,10,20 \right\\}
Hence above is the required answer.
(vii)B−C(vii)B-C
Now, we have B=\left\\{ 4,8,12,16,20 \right\\},C=\left\\{ 2,4,6,8,10,12,14,16 \right\\}
Now, the removing the elements of set C from set B we will get
\Rightarrow B-C=\left\\{ 20 \right\\}
Hence above is the required answer.
(viii)B−D(viii)B-D
Now, we have B=\left\\{ 4,8,12,16,20 \right\\},D=\left\\{ 5,10,15,20 \right\\}
Now, the removing the elements of set D from set B we will get
\Rightarrow B-D=\left\\{ 4,8,12,16 \right\\}
Hence above is the required answer.
(ix)C−B(ix)C-B
Now, we have B=\left\\{ 4,8,12,16,20 \right\\},C=\left\\{ 2,4,6,8,10,12,14,16 \right\\}
Now, the removing the elements of set B from set C we will get
\Rightarrow C-B=\left\\{ 2,6,10,14 \right\\}
Hence above is the required answer.
(x)D−B(x)D-B
Now, we have B=\left\\{ 4,8,12,16,20 \right\\},D=\left\\{ 5,10,15,20 \right\\}
Now, the removing the elements of set B from set D we will get
\Rightarrow D-B=\left\\{ 5,10,15 \right\\}
Hence above is the required answer.
(xi)C−D(xi)C-D
Now, we have C=\left\\{ 2,4,6,8,10,12,14,16 \right\\}, D=\left\\{ 5,10,15,20 \right\\}
Now, the removing the elements of set D from set C we will get
\Rightarrow C-D=\left\\{ 2,4,6,8,12,14,16 \right\\}
Hence above is the required answer.
(xii)D−C(xii)D-C
Now, we have C=\left\\{ 2,4,6,8,10,12,14,16 \right\\}, D=\left\\{ 5,10,15,20 \right\\}
Now, the removing the elements of set C from set D we will get
\Rightarrow D-C=\left\\{ 5,15,20 \right\\}

Note: Alternatively we can represent the difference of sets by using the venn diagram.
For example if we have two sets as set A and set B and we have to find the difference as B−AB-A . we can represent by using the venn diagram as

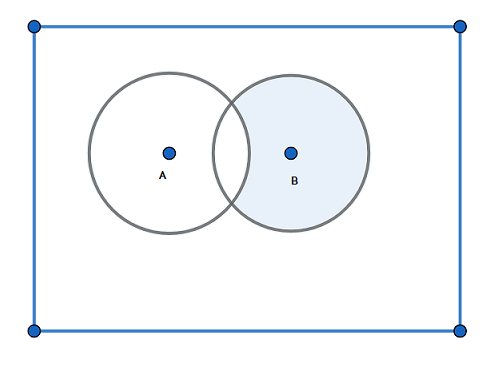
Here in the above diagram the shaded part represents B−AB-A.