Solveeit Logo
Login

Question

Question: If \[A\left( 3,4 \right)\] and \(B\left( -5,-2 \right)\) are the extremities of the base of an isosc...

If A(3,4)A\left( 3,4 \right) and B(−5,−2)B\left( -5,-2 \right) are the extremities of the base of an isosceles triangle ABC with tan⁡C=2\tan C=2 , then point C can be
(a) (35−12,−(1+25))\left( \dfrac{3\sqrt{5}-1}{2},-\left( 1+2\sqrt{5} \right) \right)
(b) (−35−52,3+25)\left( -\dfrac{3\sqrt{5}-5}{2},3+2\sqrt{5} \right)
(c) (35−12,3−25)\left( \dfrac{3\sqrt{5}-1}{2},3-2\sqrt{5} \right)
(d) (−(35−5)2,−(1−25))\left( -\dfrac{\left( 3\sqrt{5}-5 \right)}{2},-\left( 1-2\sqrt{5} \right) \right)

Explanation

Solution

Use mid-point theorem to find midpoint of AB. From ΔBCD\Delta BCD find cot⁡C2\cot \dfrac{C}{2} and find distance of BD using distance formula. Thus, find the length of the altitude CD. By using a parametric form of straight line, find coordinates of C.

Complete step by step answer:
Given that A(3,4)A\left( 3,4 \right) and B(−5,−2)B\left( -5,-2 \right) are the extreme ends of the base of the isosceles triangle ABC. Let ∠BCA\angle BCAbe the angle. Where ∠BCA=C\angle BCA=C.

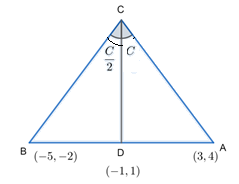
Now, let us consider D as the midpoint of base AB.
To find the coordinate of D, let us use mid-point theorem,
(X1+X22,Y1+Y22)\left( \dfrac{{{X}_{1}}+{{X}_{2}}}{2},\dfrac{{{Y}_{1}}+{{Y}_{2}}}{2} \right)
Where,
(X1,Y1)=(−5,−2) (X2,Y2)=(3,4) \begin{aligned} & \left( {{X}_{1}},{{Y}_{1}} \right)=\left( -5,-2 \right) \\\ & \left( {{X}_{2}},{{Y}_{2}} \right)=\left( 3,4 \right) \\\ \end{aligned}
∴\therefore Midpoint of AB,D=(−5+32,−2+42)=(−1,1)AB,D=\left( \dfrac{-5+3}{2},\dfrac{-2+4}{2} \right)=\left( -1,1 \right)
∴D(−1,1)\therefore D\left( -1,1 \right) is the midpoint of AB and joins CD.
Now, let us consider the right triangle BDC.
∠BCA=C ∠BCA=∠BCD+∠ACD \begin{aligned} & \angle BCA=C \\\ & \angle BCA=\angle BCD+\angle ACD \\\ \end{aligned}
The altitude CD divides ∠BCA\angle BCA into two equal halves,
∴∠BCD=∠ACD ⇒∠BCA=∠BCD+∠BCD ∠BCA=2∠BCD ∠C=2∠BCD ∴∠BCD=C2 ∴∠BCD=∠ACD=C2 \begin{aligned} & \therefore \angle BCD=\angle ACD \\\ & \Rightarrow \angle BCA=\angle BCD+\angle BCD \\\ & \angle BCA=2\angle BCD \\\ & \angle C=2\angle BCD \\\ & \therefore \angle BCD=\dfrac{C}{2} \\\ & \therefore \angle BCD=\angle ACD=\dfrac{C}{2} \\\ \end{aligned}
By using basic geometry,
tan⁡C2=opposite sideadjacent side=BDCD\tan \dfrac{C}{2}=\dfrac{\text{opposite}\ \text{side}}{\text{adjacent}\ \text{side}}=\dfrac{BD}{CD}
We know, cot⁡C2\cot \dfrac{C}{2} is the inverse of tan⁡C2\tan \dfrac{C}{2},
∴cot⁡C2=1tan⁡C2=1BDCD ∴cot⁡C2=CDBD Altitude CD=BD.cot⁡C2...........(1) \begin{aligned} & \therefore \cot \dfrac{C}{2}=\dfrac{1}{\tan \dfrac{C}{2}}=\dfrac{1}{\dfrac{BD}{CD}} \\\ & \therefore \cot \dfrac{C}{2}=\dfrac{CD}{BD} \\\ & Altitude\ CD=BD.\cot \dfrac{C}{2}...........\left( 1 \right) \\\ \end{aligned}
We have been given that tan C = 2.
By using the trigonometric formula of tan⁡θ=2tan⁡θ21−tan⁡2θ2\tan \theta =\dfrac{2\tan \dfrac{\theta }{2}}{1-{{\tan }^{2}}\dfrac{\theta }{2}}
Here, θ=C\theta =C
∴tan⁡C=2 2tan⁡C21−tan⁡2C2=2 \begin{aligned} & \therefore \tan C=2 \\\ & \dfrac{2\tan \dfrac{C}{2}}{1-{{\tan }^{2}}\dfrac{C}{2}}=2 \\\ \end{aligned}
Cross multiply and simplifying the above expression, we get,
2tan⁡C2=2[1−tan⁡2C2] 2tan⁡C2=2−2tan⁡2C2 2tan⁡2C2+2tan⁡C2−2=0 \begin{aligned} & 2\tan \dfrac{C}{2}=2\left[ 1-{{\tan }^{2}}\dfrac{C}{2} \right] \\\ & 2\tan \dfrac{C}{2}=2-2{{\tan }^{2}}\dfrac{C}{2} \\\ & 2{{\tan }^{2}}\dfrac{C}{2}+2\tan \dfrac{C}{2}-2=0 \\\ \end{aligned}
Divide the entire equation by 2.
 tan2C2+tan⁡C2−1=0.............(2)\text{ ta}{{\text{n}}^{2}}\dfrac{C}{2}+\tan \dfrac{C}{2}-1=0.............\left( 2 \right)
Here equation (2) is similar to quadratic equation whose general equation is ax2+bx+c=0a{{x}^{2}}+bx+c=0, comparing equation (2) and general equation, we get a=1,b=1, c=−1a=1,b=1,\text{ }c=-1.
Let us substitute these values in the Quadratic formula −b±b2−4ac2a\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} .

& \tan \dfrac{C}{2}=\dfrac{-1\pm \sqrt{{{1}^{2}}-4\times 1\times \left( -1 \right)}}{2\times 1} \\\ & \tan \dfrac{C}{2}=\dfrac{-1\pm \sqrt{1+4}}{2}=\dfrac{-1+\sqrt{5}}{2} \\\ & \therefore \tan \dfrac{C}{2}=\dfrac{-1+\sqrt{5}}{2}=\dfrac{\sqrt{5}-1}{2} \\\ \end{aligned}$$ Now, we need to find $\cot \dfrac{C}{2}$ which is the inverse of $\tan \dfrac{C}{2}$, so we get $$\begin{aligned} & \cot \dfrac{C}{2}=\dfrac{1}{\tan \dfrac{C}{2}}=\dfrac{1}{\dfrac{\sqrt{5}-1}{2}} \\\ & \therefore \cot \dfrac{C}{2}=\dfrac{2}{\sqrt{5}-1} \\\ \end{aligned}$$ Multiply by $\left( \sqrt{5}+1 \right)$ in the numerator & denominator. $$\begin{aligned} & \cot \dfrac{C}{2}=\dfrac{2\left( \sqrt{5}+1 \right)}{\left( \sqrt{5}-1 \right)\left( \sqrt{5}+1 \right)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \because \left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}} \\\ & =\dfrac{2\left( \sqrt{5}+1 \right)}{{{\left( \sqrt{5} \right)}^{2}}-{{1}^{2}}}=\dfrac{2\left( \sqrt{5}+1 \right)}{5-1}=\dfrac{2\left( \sqrt{5}+1 \right)}{4}=\dfrac{\sqrt{5}+1}{2} \\\ & \Rightarrow \cot \dfrac{C}{2}=\dfrac{\sqrt{5}+1}{2}.............\left( 3 \right) \\\ \end{aligned}$$ Now, let us find the length of BD. Where, $B\left( -5,-2 \right)\text{ and D}\left( -1,1 \right)$ By using the distance formula, $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ Substitute the values, $\begin{aligned} & BD=\sqrt{{{\left( -1+5 \right)}^{2}}+{{\left( 1+2 \right)}^{2}}}=\sqrt{16+9}=\sqrt{25}=5 \\\ & \therefore BD=5.........................\left( 4 \right) \\\ \end{aligned}$ Now, let us substitute the values of (3) and (4) in equation (1), we get $$\begin{aligned} & CD=BD.\cot \dfrac{C}{2} \\\ & =5\left( \dfrac{\sqrt{5}+1}{2} \right) \\\ & CD=\dfrac{5}{2}\left( \sqrt{5}+1 \right) \\\ \end{aligned}$$ We need to find the slope of BD, using the formula Slope$$=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$ $\begin{aligned} & \text{Slope of BD =}\dfrac{1-\left( -2 \right)}{-1-\left( -5 \right)}=\dfrac{3}{4} \\\ & \text{Slope of CD =}-\dfrac{1}{BD}=\dfrac{-4}{\dfrac{3}{4}}=\dfrac{-4}{3} \\\ & \therefore \tan \alpha =\dfrac{-4}{3} \\\ \end{aligned}$ The parametric form of straight line is given as $\left( {{x}_{1}}+r\cos \theta ,{{y}_{1}}+r\sin \theta \right)\ $here $\left( {{x}_{1}}{{y}_{1}} \right)=D\left( -1,1 \right)\ r=\dfrac{5}{2}\left( \sqrt{5}+1 \right)$ Thus, form the points, By using parametric form of straight line, coordinates of C are; $\begin{aligned} & \left[ -1\pm \dfrac{5}{2}\left( \sqrt{5}+1 \right)\cos \alpha ,1\pm \dfrac{5}{2}\left( \sqrt{5}+1 \right)\sin \alpha \right]\ and \\\ & \left( \dfrac{-5+3\sqrt{5}}{2},2\sqrt{5}+3 \right)and\left[ \dfrac{3\sqrt{5}-1}{2},-\left( 2\sqrt{5}+1 \right) \right] \\\ \end{aligned}$ **So, the correct answers are “Option A and B”.** **Note:** To get point C, it’s important to find the altitude CD. Remember to use a parametric form of straight line to get the final answer. Basic trigonometric formulas are also used to expand tan C. You should learn formulas so the question becomes easy to solve.