Solveeit Logo
Login

Question

Question: If \(A\left( 3,2,0 \right),B\left( 5,3,2 \right)\And C\left( -9,6,-3 \right)\) are the vertices of \...

If A(3,2,0),B(5,3,2)&C(−9,6,−3)A\left( 3,2,0 \right),B\left( 5,3,2 \right)\And C\left( -9,6,-3 \right) are the vertices of ΔABC\Delta ABC and the bisector of ∠BAC\angle BAC meets BC at D, then coordinates of D are:
(a) (198,5716,1716)\left( \dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right)
(b) (−198,5716,1716)\left( -\dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right)
(c) (198,−5716,1716)\left( \dfrac{19}{8},-\dfrac{57}{16},\dfrac{17}{16} \right)
(d) None of these

Explanation

Solution

First of all draw a ΔABC\Delta ABC and then draw the angle bisector of angle A. The angle bisector of angle A meets BC at point D. Now, the ratio of BD and DC is equal to the ratio of AB and AC. We know the coordinates of A, B and C so using the distance formula we can find the distances AB and AC. The distance formula for two points say P(x1,y1,z1)&Q(x2,y2,z2)P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\And Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) is (x2−x1)2+(y2−y1)2+(z2−z1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}. Substitute the lengths of AB and AC in the ratio equation after substitution you will get the ratio in which point D divides B and C then using the section formula we will find the coordinates of D.

Complete step by step answer:
In the below figure, we have drawn a triangle ABC with an angle bisector of angle A which meets BC at D.

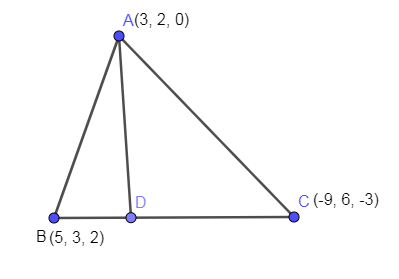
There is a property of angle bisectors that it divides the opposite side in the ratio equal to the ratio of the remaining sides.
BDDC=ABAC\dfrac{BD}{DC}=\dfrac{AB}{AC} ………….Eq. (1)
Now, using the distance formula of the two points we are going to find the distances of AB and AC.
The distance formula between two points say P(x1,y1,z1)&Q(x2,y2,z2)P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\And Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) is equal to:
(x2−x1)2+(y2−y1)2+(z2−z1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}
Using this distance formula, we are going to find the distance between A and B, distance between A and C.
The coordinates of points A and B are A(3,2,0),B(5,3,2)A\left( 3,2,0 \right),B\left( 5,3,2 \right) and distance between them is equal to:
(5−3)2+(3−2)2+(2−0)2 =(2)2+(1)2+(2)2 =4+1+4 =9=3 \begin{aligned} & \sqrt{{{\left( 5-3 \right)}^{2}}+{{\left( 3-2 \right)}^{2}}+{{\left( 2-0 \right)}^{2}}} \\\ & =\sqrt{{{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}+{{\left( 2 \right)}^{2}}} \\\ & =\sqrt{4+1+4} \\\ & =\sqrt{9}=3 \\\ \end{aligned}
Hence, the length of AB is equal to 3.
The coordinates of A and C are A(3,2,0),C(−9,6,−3)A\left( 3,2,0 \right),C\left( -9,6,-3 \right) and distance between them is equal to:
(−9−3)2+(6−2)2+(−3−0)2 =(−12)2+(4)2+(−3)2 =144+16+9 =169=13 \begin{aligned} & \sqrt{{{\left( -9-3 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}+{{\left( -3-0 \right)}^{2}}} \\\ & =\sqrt{{{\left( -12 \right)}^{2}}+{{\left( 4 \right)}^{2}}+{{\left( -3 \right)}^{2}}} \\\ & =\sqrt{144+16+9} \\\ & =\sqrt{169}=13 \\\ \end{aligned}
Hence, the length of AC is equal to 13.
Now, substituting the values of AB and AC in eq. (1) we get,
BDDC=313\dfrac{BD}{DC}=\dfrac{3}{13}
The above equation shows that the point D divides the side BC into the ratio of 3:13 so using section formula we can find the coordinates of point D.
Section formula for point R that divides the two points say P(x1,y1,z1)&Q(x2,y2,z2)P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\And Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) in the ratio of m1:m2{{m}_{1}}:{{m}_{2}} so the coordinates R is calculated as follows:
(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2,m1z2+m2z1m1+m2)\left( \dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{z}_{2}}+{{m}_{2}}{{z}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)
The coordinates of B and C is given as B(5,3,2)&C(−9,6,−3)B\left( 5,3,2 \right)\And C\left( -9,6,-3 \right) with a ratio of 3:13 so using the above section formula we can find the coordinates of point D as:
D(3(−9)+13(5)16,3(6)+13(3)16,3(−3)+13(2)16) =D(−27+6516,18+3916,−9+2616) =D(3816,5716,1716) =D(198,5716,1716) \begin{aligned} & D\left( \dfrac{3\left( -9 \right)+13\left( 5 \right)}{16},\dfrac{3\left( 6 \right)+13\left( 3 \right)}{16},\dfrac{3\left( -3 \right)+13\left( 2 \right)}{16} \right) \\\ & =D\left( \dfrac{-27+65}{16},\dfrac{18+39}{16},\dfrac{-9+26}{16} \right) \\\ & =D\left( \dfrac{38}{16},\dfrac{57}{16},\dfrac{17}{16} \right) \\\ & =D\left( \dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right) \\\ \end{aligned}

So, the correct answer is “Option a”.

Note: The mistake that could happen is in writing the section formula. In the below, we have written the section formula as:
(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2,m1z2+m2z1m1+m2)\left( \dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}},\dfrac{{{m}_{1}}{{z}_{2}}+{{m}_{2}}{{z}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)
The confusion in writing the above formula is that whether m1{{m}_{1}} is written with x1{{x}_{1}} or x2{{x}_{2}} and similarly with which x value m2{{m}_{2}} should be written. Similarly, for y and z also this problem occurs. The solution to this confusion is either m1{{m}_{1}} or m2{{m}_{2}} the subscript of x should be different from the subscript of m. For instance, in the above formula we have written m1{{m}_{1}} with x2{{x}_{2}} so here you can see that subscript of m is 1 and subscript of x is 2 which are different from each other. Likewise you can remember for y and z also.