Question

If A is square matrix and $A^2 + I = 2A$, then $A^9 =$

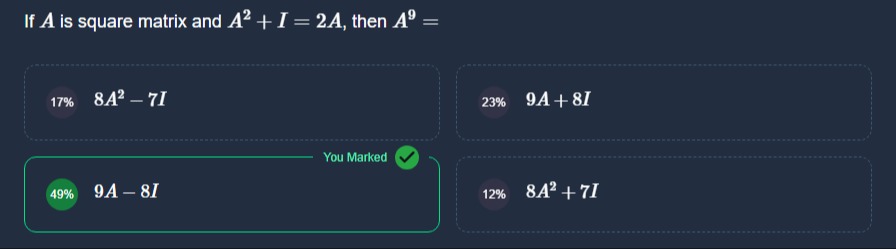
• A. $8A^2 - 7I$
• B. $9A + 8I$
• C. $9A - 8I$
• D. $8A^2 + 7I$

Answer 1

Answer: (C)

9A - 8I

Answer 2

Solution:

We are given:

$$A^2 + I = 2A \quad \Rightarrow \quad A^2 - 2A + I = 0 \quad \Rightarrow \quad (A-I)^2 = 0.$$

This means that $A-I$ is nilpotent of index 2.

To find $A^9$, first note from the equation:

$$A^2 = 2A - I.$$

We can compute:

$$\begin{aligned} A^3 &= A \cdot A^2 = A(2A-I)=2A^2-A\\ &=2(2A-I)-A\\ &=4A-2I-A\\ &=3A-2I. \end{aligned}$$

One can see a pattern: assume that

$$A^n = nA-(n-1)I.$$

This holds for $n=1$ and $n=2$. Assuming it holds for $n$, then

$$\begin{aligned} A^{n+1} &= A \cdot A^n = A(nA-(n-1)I)\\ &= nA^2 - (n-1)A\\ &= n(2A-I) - (n-1)A\\ &= (2n-(n-1))A - nI\\ &= (n+1)A - nI. \end{aligned}$$

Thus by induction, the pattern is valid.

For $n=9$:

$$A^9 = 9A-8I.$$

So, the correct option is 9A - 8I.

---

Core Explanation:

1. Rearranged given equation to $A^2-2A+I=0$ $\Rightarrow$ $(A-I)^2=0$.
2. Found by induction that $A^n=nA-(n-1)I$.
3. Substituted $n=9$ to get $A^9=9A-8I$.