Question

If A is a subset of B, then which of the following is correct?

$$\left( A \right){A^c} \subseteq {B^c} \\\ \left( B \right){B^c} \subseteq {A^c} \\\ \left( C \right){A^c} = {B^c} \\\ \left( D \right)A \subseteq A \cap B \\\$$

Answer 1

We solve this type of problem by using two methods . The first method is by taking an example and checking every option given in the problem and the second method is by using Venn diagrams .

Complete step-by-step answer:
The objective of the problem is to find the correct option from the given options.
This problem can be solved by two methods: they are verifying the options and the other one is by using Venn diagrams.
Method 1: By checking the given options
Given that A is the subset of B.
Let us consider the universal set denoted by U as U = \left\\{ {a,b,c,d,e,f,g,h} \right\\}
Let us consider the two sets A and B where A is the set of elements a,b,c,d and B is the set of elements a,b,c,d,e. The usual notation of sets A and B is A = \left\\{ {a,b,c,d} \right\\},\,B = \left\\{ {a,b,c,d,e} \right\\}.
Now find A compliment and B complement.
${A^c}$is defined as the set of all elements present in the universal set except the elements present in set A.
That is {A^c} = \left\\{ {e,f,g,h} \right\\}
Similarly , ${B^c}$ is defined as the set of all elements present in the universal set except the elements present in the set B.
That is , {B^c} = \left\\{ {f,g,h} \right\\}
Now find the $A \cap B$. A intersection B is defined as the set of all elements that are common in the given two sets A and B.
That is A \cap B = \left\\{ {a,b,c,d} \right\\}
Now check the options given .First let us check option A .The option A is false because it is given that A is subset of B .Although the elements of ${A^c}$ is contained in ${B^c}$ the option is not satisfying the given if condition . Option B is true because the elements in ${B^c}$ are contained in ${A^c}$ and also satisfy the given condition. Similarly options C and D are also not correct .
Therefore, option B that is ${B^c} \subseteq {A^c}$ is correct.
Method 2: By using Venn diagrams
The Venn diagram of $A \subset B$ is

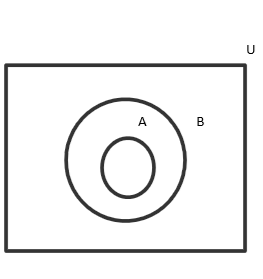
The Venn diagram for ${A^c}$ is

The Venn diagram for ${B^c}$ is

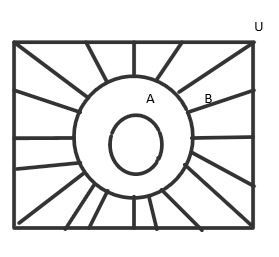
It is clear from the diagrams that ${B^c} \subseteq {A^c}$.
Thus , option B is correct.

Note: Union is defined as the set of all elements that are contained in one and each other . A subset is defined as a set of which all the elements are contained in another set. Every set is subset to itself and the empty set is subset to every set.