Question
Question: If A is a square matrix of order n x n and k is a scalar, then adj(kA) is equal to...
If A is a square matrix of order n x n and k is a scalar, then adj(kA) is equal to
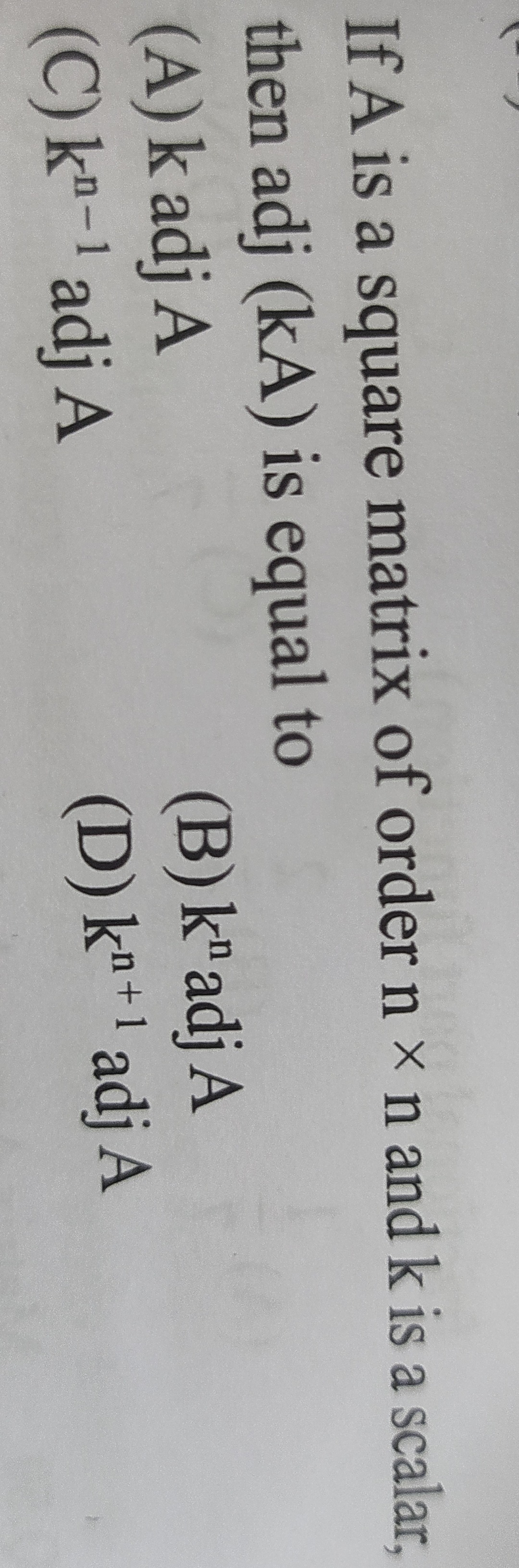
k adj A
kn adj A
kn−1 adj A
kn+1 adj A
kn−1 adj A
Solution
Let A be a square matrix of order n x n and k be a scalar. We want to find adj(kA).
We know that for any square matrix M, M(adj M)=(adj M)M=det(M)In, where In is the identity matrix of order n.
Let M = kA. Then (kA)adj(kA)=det(kA)In.
We also know the property that for a scalar k and an n x n matrix A, det(kA)=kndet(A).
Substituting this into the equation, we get:
(kA)adj(kA)=kndet(A)In.
We also know that A(adj A)=det(A)In.
If A is invertible, then det(A)=0, and A−1=det(A)1adj A.
Also, if k=0, then kA is invertible if and only if A is invertible.
If k=0 and A is invertible, then (kA)−1=k−1A−1.
Multiply the equation (kA)adj(kA)=kndet(A)In by (kA)−1 from the left:
(kA)−1(kA)adj(kA)=(kA)−1kndet(A)In
Inadj(kA)=(k−1A−1)kndet(A)
adj(kA)=kn−1A−1det(A)
Since A−1det(A)=adj A, we have:
adj(kA)=kn−1adj A.
