Question
Question: If $A$ is a square matrix of order 3 such that $|A|=5$ then $|(adjA^{-1})^{-1}|$ is...
If A is a square matrix of order 3 such that ∣A∣=5 then ∣(adjA−1)−1∣ is
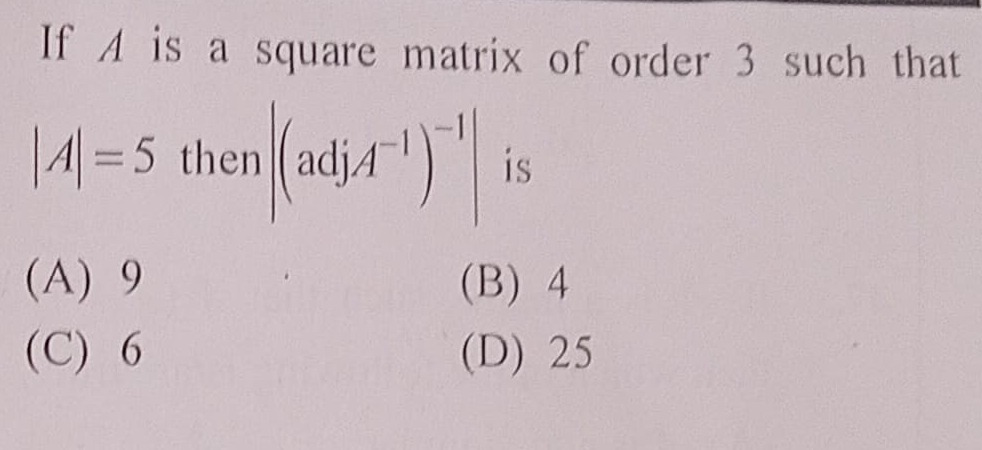
9
4
6
25
25
Solution
Let A be a square matrix of order n=3. Given ∣A∣=5. We need to find the value of ∣(adjA−1)−1∣.
We will use the following properties of matrices and determinants:
-
For any invertible matrix X, (X−1)−1=X.
-
For an invertible matrix X, adj(X−1)=(adjX)−1.
-
For a square matrix X of order n, ∣adjX∣=∣X∣n−1.
Now, let's simplify the given expression step-by-step:
-
Step 1: Apply the property adj(X−1)=(adjX)−1 with X=A. So, adj(A−1)=(adjA)−1. The expression becomes ∣(adj(A−1))−1∣=∣((adjA)−1)−1∣.
-
Step 2: Apply the property (Y−1)−1=Y with Y=adjA. So, ((adjA)−1)−1=adjA. The expression simplifies to ∣adjA∣.
-
Step 3: Apply the property ∣adjA∣=∣A∣n−1. Given that the order of matrix A is n=3. So, ∣adjA∣=∣A∣3−1=∣A∣2.
-
Step 4: Substitute the given value of ∣A∣. Given ∣A∣=5. Therefore, ∣adjA∣=(5)2=25.
Thus, ∣(adjA−1)−1∣=25.
