Question

If A is a non-singular matrix such that $(A-2I)(A-3I) = O$, then $\frac{1}{5}A + \frac{6}{5}A^{-1} =$

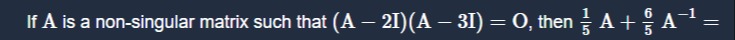
• A. 0
• B. I
• C. A
• D. A^{-1}

Answer 1

Answer: (B)

I

Answer 2

Given $(A - 2I)(A - 3I) = O$, expand the product:

$A^2 - 5A + 6I = O \implies A^2 = 5A - 6I$.

Multiplying by $A^{-1}$ (since $A$ is non-singular) yields:

$A = 5I - 6A^{-1} \implies A + 6A^{-1} = 5I$.

Dividing both sides by 5:

$\frac{1}{5}A + \frac{6}{5}A^{-1} = I$.