Solveeit Logo
Login

Question

Question: If A is (5, -2), B is (2, 4) and point C lies on the locus whose equation is \( y = 1 + x + {x^2} \)...

If A is (5, -2), B is (2, 4) and point C lies on the locus whose equation is y=1+x+x2y = 1 + x + {x^2} , find the equation of the locus of centroid of △ABC\vartriangle ABC

Explanation

Solution

Hint : We have been given the equation of locus of point C, using this, we can find the equation of centroid consisting of its coordinates which can be calculated using the formula for centroid. As the equation of locus is always given by x and y coordinates and hence respective conversions can be made to get the required equation.
(h,k)=(x1+x2+x33,y1+y2+y33)(h,k) = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right) where x and y denotes the coordinates of the 3 vertices respectively and h, k are the coordinates of centroid.

Complete step-by-step answer :
The point A and B of the triangle is given to be (5, -2) and (2, 4) respectively. Let the point C be (x, y) and centroid of the triangle be (h, k)

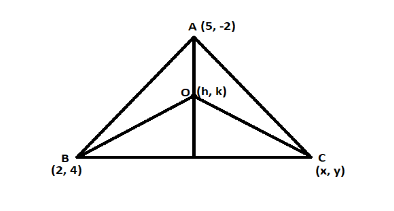
The centroid of the triangle is given as:
(h,k)=(x1+x2+x33,y1+y2+y33)(h,k) = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)
Substituting the values of vertices in respective axes from the diagram, we get:
(h,k)=(5+2+x3,−2+4+y3) (h,k)=(x+73,y+23) ⇒h=x+73;k=y+23 ⇒x=3h−7;y=3k−2 ⇒(x,y)=(3h−7,3k−2)   (h,k) = \left( {\dfrac{{5 + 2 + x}}{3},\dfrac{{ - 2 + 4 + y}}{3}} \right) \\\ (h,k) = \left( {\dfrac{{x + 7}}{3},\dfrac{{y + 2}}{3}} \right) \\\ \Rightarrow h = \dfrac{{x + 7}}{3};k = \dfrac{{y + 2}}{3} \\\ \Rightarrow x = 3h - 7;y = 3k - 2 \\\ \Rightarrow (x,y) = (3h - 7,3k - 2) \;
It is given that point C lies on the locus whose equation is y=1+x+x2y = 1 + x + {x^2} .
We have found the value of coordinates (x, y) of C in terms of coordinates of centroid (h, k), substituting we get:
y=1+x+x2 ⇒3k−2=1+3h−7+(3h−7)2 (∵x=3h−7 ,y=3k−2 ) ⇒3k−3=3h−7+9h2−42h+49 ⇒9h2−39h−3k+45   y = 1 + x + {x^2} \\\ \Rightarrow 3k - 2 = 1 + 3h - 7 + {\left( {3h - 7} \right)^2} \\\ \left( \because x = 3h - 7 \ , y = 3k - 2 \ \right) \\\ \Rightarrow 3k - 3 = 3h - 7 + 9{h^2} - 42h + 49 \\\ \Rightarrow 9{h^2} - 39h - 3k + 45 \;
This is the equation with the coordinates of the centroid. But the equation of locus is always given by x and y coordinates. So, in the obtained equation, we replace h by x and k by y.
9x2−39x−3y+459{x^2} - 39x - 3y + 45
Therefore, the equation of the locus of centroid of △ABC\vartriangle ABC is 9x2−39x−3y+459{x^2} - 39x - 3y + 45 .

Note : The centroid of triangle is drawn where all the three medians from respective vertices intersect. The locus is not a particular point but a set of points sharing the same properties, it is usually a curve or a surface. Thus, it is represented by x and y coordinates in general. We found the value of h and k by equating the like quantities on both L.H.S and R.H.S of the equation and we have to follow this thing to get values of particular quantities.