Question

If $a=i+j+k$ , $b=i+3j+3k$ and $c=7i+9j+11k$ , then the area of parallelogram having diagonals $a+b$ and $b+c$ is ?

1. $4\sqrt{6}$ units
2. $\dfrac{1}{2}\left( \sqrt{21} \right)$ sq. units
3. $\dfrac{\sqrt{6}}{2}$ sq. units
4. $6$ sq. units

Answer 1

Here in this question we have been asked to find the area of parallelogram having diagonals $a+b$ and $b+c$ given that $a=i+j+k$ , $b=i+3j+3k$ and $c=7i+9j+11k$. We know that the area of parallelogram having diagonals $p$ and $q$ is given as $\dfrac{1}{2}\left| p\times q \right|$ .

Complete step by step answer:
Now considering from the question we have been asked to find the area of parallelogram having diagonals $a+b$ and $b+c$ given that $a=i+j+k$ , $b=i+3j+3k$ and $c=7i+9j+11k$.

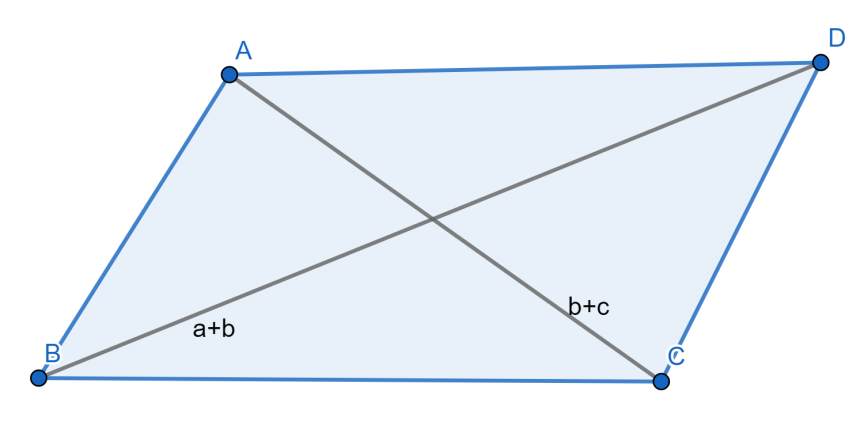
From the basic concepts, we know that the area of parallelogram having diagonals $p$ and $q$ is given as $\dfrac{1}{2}\left| p\times q \right|$ .
The cross product of any two vectors $pi+qj+rk$ and $li+mj+nk$ can be given as $\left| \begin{matrix} i & j & k \\\ p & q & r \\\ l & m & n \\\ \end{matrix} \right|$ .
Now we will evaluate the diagonals of the parallelogram in vector form.
Here the diagonals are
$\begin{aligned} & a+b=i+j+k+i+3j+3k \\\ & \Rightarrow a+b=2i+4j+4k \\\ \end{aligned}$
And
$\begin{aligned} & b+c=i+3j+3k+7i+9j+11k \\\ & \Rightarrow b+c=8i+12j+14k \\\ \end{aligned}$ .
Now we will evaluate the area of the given parallelogram as
$\begin{aligned} & \dfrac{1}{2}\left| \left( a+b \right)\times \left( b+c \right) \right|\Rightarrow \dfrac{1}{2}\left| \begin{matrix} i & j & k \\\ 2 & 4 & 4 \\\ 8 & 12 & 14 \\\ \end{matrix} \right| \\\ & \Rightarrow \dfrac{1}{2}\left( i\left( 56-48 \right)-j\left( 28-32 \right)+k\left( 24-32 \right) \right) \\\ & \Rightarrow 4i+2j-4k \\\ \end{aligned}$.
Hence we can say that the area of the given parallelogram is $\sqrt{16+4+16}=6$ .
Therefore we can conclude that the area of the given parallelogram having diagonals $a+b$ and $b+c$ given that $a=i+j+k$ , $b=i+3j+3k$ and $c=7i+9j+11k$ is 6 sq. units.
So, the correct answer is “Option 4”.

Note: In the process of answering questions of this type we should be sure with the concepts that we are going to apply and the calculations that we are going to perform in between the steps. Here if someone has considered $b=i+3j+5k$ by overlook, then they will have the area of the parallelogram as $4\sqrt{6}$ sq. units which is a wrong answer. So be careful with the calculations.