Question

If a hyperbola has a length of its conjugate axis equal to 5 and the distance between its foci is 13, then the eccentricity of the hyperbola is:
(a).2
(b).$\dfrac{13}{6}$
(c). $\dfrac{13}{8}$
(d).$\dfrac{13}{12}$

Answer 1

First of all, we will use the standard notation to denote the length of the conjugate axis, eccentricity, transverse axis.
Our approach is to first, we will calculate the length of the transverse axis, using the length between two foci and then we calculate then eccentricity of the hyperbola.
Length of transverse axis:2a
Length of conjugate axis:2b
Eccentricity: e.
The length between the two foci:2ae.

Complete step-by-step solution:
Next, we formulate two equations from the given information.

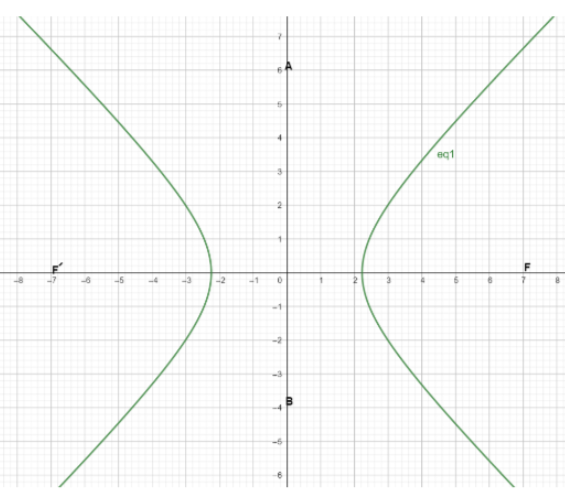
Here F and F’ are two foci, AB is a conjugate axis.
$\begin{aligned} & 2ae=13 \\\ & take\text{ both side square ,} \\\ & \text{4}{{\text{a}}^{2}}{{e}^{2}}=169 \\\ & Next\text{ we will use the fourmula for eccentricity }{{\text{e}}^{2}}=1+\dfrac{{{b}^{2}}}{{{a}^{2}}} \\\ & 4{{a}^{2}}\left( 1+\dfrac{{{b}^{2}}}{{{a}^{2}}} \right)=169 \\\ & \Rightarrow 4{{a}^{2}}+4{{b}^{2}}=169 \\\ & \Rightarrow {{a}^{2}}+{{b}^{2}}=\dfrac{169}{4} \\\ \end{aligned}$
$\Rightarrow {{a}^{2}}+{{b}^{2}}=\dfrac{169}{4}...........................................\text{(1)}$
Next we know that,
$2b=5$
$\Rightarrow b=\dfrac{5}{2}$
$\Rightarrow {{b}^{2}}=\dfrac{25}{4}..........................................(2)$
Put the value of ${{b}^{2}}$ on the equation (1), we get,
${{a}^{2}}=\dfrac{169}{4}-\dfrac{25}{4}$
$\Rightarrow {{a}^{2}}=\dfrac{144}{4}.....................................(3)$
From (2) & (3) we got the values of “${{a}^{2}}\And {{b}^{2}}$” and use the formula of eccentricity we get ,

& \\\ & e=\sqrt{1+\dfrac{{{\left( \dfrac{5}{2} \right)}^{2}}}{{{\left( \dfrac{12}{2} \right)}^{2}}}} \\\ & \Rightarrow e=\sqrt{1+\dfrac{25}{144}} \\\ & \Rightarrow e=\dfrac{13}{12} \\\ \end{aligned}$$ Hence, option (D) is correct. We are done. **Note:** First thing that you have to keep in mind the formula for the eccentricity, as if you are unable to memorize the formula, then it is going to be very tedious to prove the formula and then use it. The next point to note is the in equation (1), when we substitute the value of “b”, in order to get “a”, we can also substitute the value of “a” in terms of “e” and find directly get the value of eccentricity.