Solveeit Logo
Login

Question

Question: If a given base triangle is described such that the sum of the tangents of the base angles is consta...

If a given base triangle is described such that the sum of the tangents of the base angles is constant, prove that the locus of the vertices is a parabola.

Explanation

Solution

Hint: We need to take the given condition in co-ordinate plane and use tan⁡θ=perpendicularbase\tan \theta =\dfrac{\text{perpendicular}}{\text{base}} in different triangles

Complete step-by-step answer:
Given that the sum of the tangents of base angles of the triangle is constant. We have to prove that the locus of the vertices is a parabola.

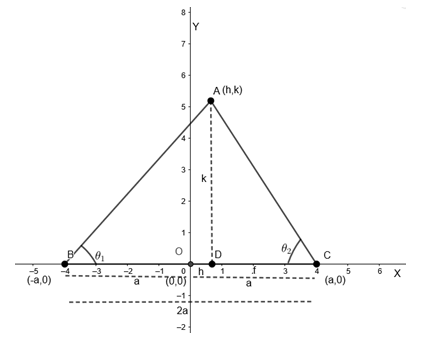
Let the given base of the triangle is BC of length 2a. Also let the coordinates of C be (a, 0) and B be (-a, 0) such that OB = OC = a.
We have to prove that the locus of A is parabola, so let the coordinates of A be (h, k).
Hence, we get OD = h and AD = k.
Also, given that the sum of tangents of angles B and C are constant.
Hence, we get tan⁡θ1+tan⁡θ2=C....(i)[C = constant]\tan {{\theta }_{1}}+\tan {{\theta }_{2}}=C....\left( i \right)\left[ \text{C = constant} \right]
We know that tan⁡θ=perpendicularbase\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}
Therefore, tan⁡θ1=ADBD=ka+h\tan {{\theta }_{1}}=\dfrac{AD}{BD}=\dfrac{k}{a+h}
And tan⁡θ2=ADDC=ka−h\tan {{\theta }_{2}}=\dfrac{AD}{DC}=\dfrac{k}{a-h}
Now, we will put these values in equation (i).
We get tan⁡θ1+tan⁡θ2=C\tan {{\theta }_{1}}+\tan {{\theta }_{2}}=C
⇒ka+h+ka−h=C\Rightarrow \dfrac{k}{a+h}+\dfrac{k}{a-h}=C
⇒k(a−h)+k(a+h)(a+h)(a−h)=C\Rightarrow \dfrac{k\left( a-h \right)+k\left( a+h \right)}{\left( a+h \right)\left( a-h \right)}=C
Cross Multiplying above equation, we know that,
(x+y)(x−y)=x2−y2\left( x+y \right)\left( x-y \right)={{x}^{2}}-{{y}^{2}}
We get, 2ka=C(a2−h2)2ka=C\left( {{a}^{2}}-{{h}^{2}} \right)
By rearranging the equation, we get,
Ch2=Ca2−2kaC{{h}^{2}}=C{{a}^{2}}-2ka
⇒h2=−2aC[k−Ca2]\Rightarrow {{h}^{2}}=\dfrac{-2a}{C}\left[ k-\dfrac{Ca}{2} \right]
Replacing h by x and k by y for the locus
⇒x2=−2aC[y−Ca2]\Rightarrow {{x}^{2}}=\dfrac{-2a}{C}\left[ y-\dfrac{Ca}{2} \right]
which is comparable to parabola.
(x−x1)2=−4a(y−y1){{\left( x-{{x}_{1}} \right)}^{2}}=-4a\left( y-{{y}_{1}} \right)
Hence, we proved that the locus of vertices is a parabola.

Note: Instead of taking arbitrary points, we must take the points in co-ordinate plane like we did in this question to make the question easily solvable. We must rearrange the equation until we get the desired form.