Question

If a function is given as $f'(x)=|x|-\\{x\\}$ where $\\{x\\}$ is the fractional part of x, then f(x) is increasing in:
(a) $\left( 0,1 \right)$
(b) $\left( \dfrac{-1}{2},0 \right)$
(c) $\left( \dfrac{1}{2},2 \right)$
(d) $\left( \dfrac{1}{2},\infty \right)$

Answer 1

Hint : We know that the condition for an increasing function in an interval is $f'(x)>0$ at every point in that interval. We find an interval for x in which condition $f'(x)>0$ is satisfied. In order to find the interval we use the fact that \left\\{ x \right\\}=x-\left[ x \right] for all x, where $\left[ . \right]$ is Greatest Integer Function and properties of $\left| x \right|=x$ for $x>0$ , $\left| x \right|=-x$ for $x<0$ .

Complete step-by-step answer :
Given that $f'(x)=|x|-\\{x\\}$ , where $\\{x\\}$ is the fractional part of x.
We need to find the interval in which f(x) is increasing.
We know that for a f(x) to become an increasing function in a given interval the following condition needs to be satisfied.
$f'(x)>0$
According to the problem $f'(x)=|x|-\\{x\\}$ . So,
$|x|-\\{x\\}>0$
We know that fractional part of x ({x}) is defined as follows
Fractional part$\\{x\\}=x-[x]$, where [.] is Greatest Integer function.
$\left| x \right|-\left( x-\left[ x \right] \right)>0.......(1)$
Since properties of modulus of x (|x|) changes with respect to value of x. We divide into two conditions for ‘x’ as follows:
$1)x<0$
$2)x>0$
Let us first find the interval for f(x) using condition (1).
We know for $x<0$ , $|x|=-x$ .
Let us use this in equation (1).
$-x-(x-[x])>0$
$-2x+[x]>0$
$[x]>2x$
Since $x<0$ and $\left[ x \right]$ takes the value of the greatest integer less than or equal to the value of x it varies from -1 to $-\infty$ . So, we get $2x<-1$ .
$x<\dfrac{-1}{2}$ .
We got $f'(x)>0$ in the interval $\left( -\infty ,\dfrac{-1}{2} \right)$ .
Now we find the interval for f(x) using condition (2).
We know that for $x>0$ ,|x|=x.
Let us use this in equation (1).
$x-(x-[x])$ >0
$x-x+[x]>0$
$[x]>0$
Since $x>0$ and $[x]$ takes the value of the greatest integer less than or equal to the value of x, it varies from 0 to $+\infty$ .
We also know that $[x]=0$ in the interval $[0,1)$ .
So, we understood that x>1.
The interval in which $f'(x)>0$ is $[1,\infty )$ .
∴ The interval in which $f'(x)>0$ is $\left( -\infty ,\dfrac{-1}{2} \right)\bigcap \left[ 1,\infty \right)$
We don’t have a correct option.

Note : Alternatively we can draw the plots of $\left| x \right|$ and \left\\{ x \right\\} to check $f'(x)>0$ . Now we solve by using the idea for an alternative solution.
We know that for a f(x) to become an increasing function in a given interval the following condition needs to be satisfied.
$f'(x)>0......(1)$
We have $f'(x)=|x|-\\{x\\}$ as given in the problem.
Using equation (1), we get \left| x \right|-\left\\{ x \right\\}>0
\left| x \right|>\left\\{ x \right\\}......(2)
Now from the plot we need to find the interval where condition in equation (2) holds true.
Let us plot curves $y=\left| x \right|$ and y=\left\\{ x \right\\} .

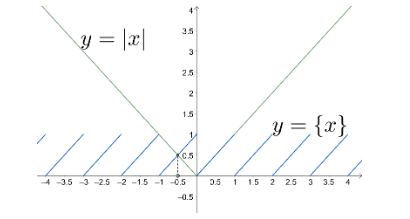
From above graph, we can observe that the value of $\left| x \right|$ is greater than \left\\{ x \right\\} in interval $\left( -\infty ,\dfrac{-1}{2} \right)\bigcap \left[ 1,\infty \right)$ .
You may confuse here as both plots coincide with each other in interval $\left( 0,1 \right)$ . This makes $f'(x)=0$ which eventually makes f(x) constant in that interval.