Question

If a function is defined on $f:\left( e,\infty \right]\to R$ as $f\left( x \right)=\ln \left( \ln \left( \ln \left( x \right) \right) \right)$, then which of the following options is true for function f?
(a) one-one into
(b) one-one onto
(c) Many-one into
(d) Many-one onto

Answer 1

We start solving the problem by recalling the definitions of one-one function, many one functions, onto and into function. We then find the derivative of a given function and find the range of it in the given domain which tells us whether the given function is one-one or not. We then find the limits at the extremums of the domain to find the range of the function. We then compare this range with the codomain to find whether the given function is onto or not.

Complete step-by-step solution
According to the problem, we are given that the function is defined on $f:\left( e,\infty \right]\to R$ as $f\left( x \right)=\ln \left( \ln \left( \ln \left( x \right) \right) \right)$ and we need to find whether the given function is one-one or onto.
Let us recall the definitions of one-one function, many one functions, onto and into function.
One-one function: A function is defined as one-one if every element of the function’s codomain is the image of at most one element of its domain.
Many-one function: A function is defined as many-one if every element of the function’s codomain is the image of one or more elements of its domain.
Onto function: A function is defined as onto if the range of the function is equal to its co-domain.
Into function: A function is defined as if the range of the function is not equal to its co-domain.
Let us find the derivative of $f\left( x \right)=\ln \left( \ln \left( \ln \left( x \right) \right) \right)$.
$\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( \ln \left( \ln \left( \ln \left( x \right) \right) \right) \right)$.
$\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{1}{\ln \left( \ln \left( x \right) \right)}\dfrac{d}{dx}\left( \ln \left( \ln \left( x \right) \right) \right)$.
$\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{1}{\ln \left( \ln \left( x \right) \right)}\times \dfrac{1}{\ln \left( x \right)}\dfrac{d}{dx}\left( \ln \left( x \right) \right)$.
$\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{1}{\ln \left( \ln \left( x \right) \right)}\times \dfrac{1}{\ln \left( x \right)}\times \dfrac{1}{x}$.
$\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{1}{x\ln \left( x \right)\ln \left( \ln \left( x \right) \right)}$.
We know that the domain of x is $x>e$ and we know that the value of $\ln \left( x \right)$ is greater than 0 in this interval, which gives us $x\ln \left( x \right)\ln \left( \ln \left( x \right) \right)>0$.
So, we get ${{f}^{'}}\left( x \right)>0$. We know that if ${{f}^{'}}\left( x \right)>0$ for all the values of x in its domain, then the function is increasing in its domain.
We know that the increasing functions $f\left( x \right)$ will give different values for different values of x, which is the property of the one-one function.
So, this gives us that the function $f\left( x \right)=\ln \left( \ln \left( \ln \left( x \right) \right) \right)$ is an one-one function ---(1).
Now, let us find the range of function $f\left( x \right)$ at extremums of domain i.e., at $x=e$ and $x=\infty$.
So, let us find the limits of these functions.
So, we get $\displaystyle \lim_{x \to {{e}^{+}}}f\left( x \right)=\displaystyle \lim_{x \to {{e}^{+}}}\ln \left( \ln \left( \ln \left( x \right) \right) \right)$ (function is not defined before $x=e$).
$\Rightarrow \displaystyle \lim_{x \to {{e}^{+}}}f\left( x \right)=\ln \left( \ln \left( \ln \left( e \right) \right) \right)$.
$\Rightarrow \displaystyle \lim_{x \to {{e}^{+}}}f\left( x \right)=\ln \left( \ln \left( 1 \right) \right)$.
$\Rightarrow \displaystyle \lim_{x \to {{e}^{+}}}f\left( x \right)=\ln \left( 0 \right)$.
$\Rightarrow \displaystyle \lim_{x \to {{e}^{+}}}f\left( x \right)=-\infty$ ---(2).
Now, let us find $\displaystyle \lim_{x \to \infty }f\left( x \right)=\displaystyle \lim_{x \to \infty }\ln \left( \ln \left( \ln \left( x \right) \right) \right)$.
$\Rightarrow \displaystyle \lim_{x \to \infty }f\left( x \right)=\ln \left( \ln \left( \ln \left( \infty \right) \right) \right)$.
$\Rightarrow \displaystyle \lim_{x \to \infty }f\left( x \right)=\ln \left( \ln \left( \infty \right) \right)$.
$\Rightarrow \displaystyle \lim_{x \to \infty }f\left( x \right)=\ln \left( \infty \right)$.
$\Rightarrow \displaystyle \lim_{x \to \infty }f\left( x \right)=\infty$ ---(3).
From equations (2) and (3), we can see that the range of the function is $\left( -\infty ,\infty \right)$ which is equal to $R$ (Co-domain).
So, we have found that the range of the function is equal to its co-domain which is the property of onto function.
So, we have found that the given function is onto ---(4).
From equations (1) and (4), we get that the given function $f\left( x \right)=\ln \left( \ln \left( \ln \left( x \right) \right) \right)$ is one-one and onto.
The correct option for the given problem is (b).

Note: We should check the domain of the function as some of the functions will be defined in a specific interval. If the domain is given as $R$, then the given $f\left( x \right)$ cannot be told as a function as it is not defined in the interval $x\le e$. Alternatively, we can solve this problem by drawing the graph of the given function which is as shown below:

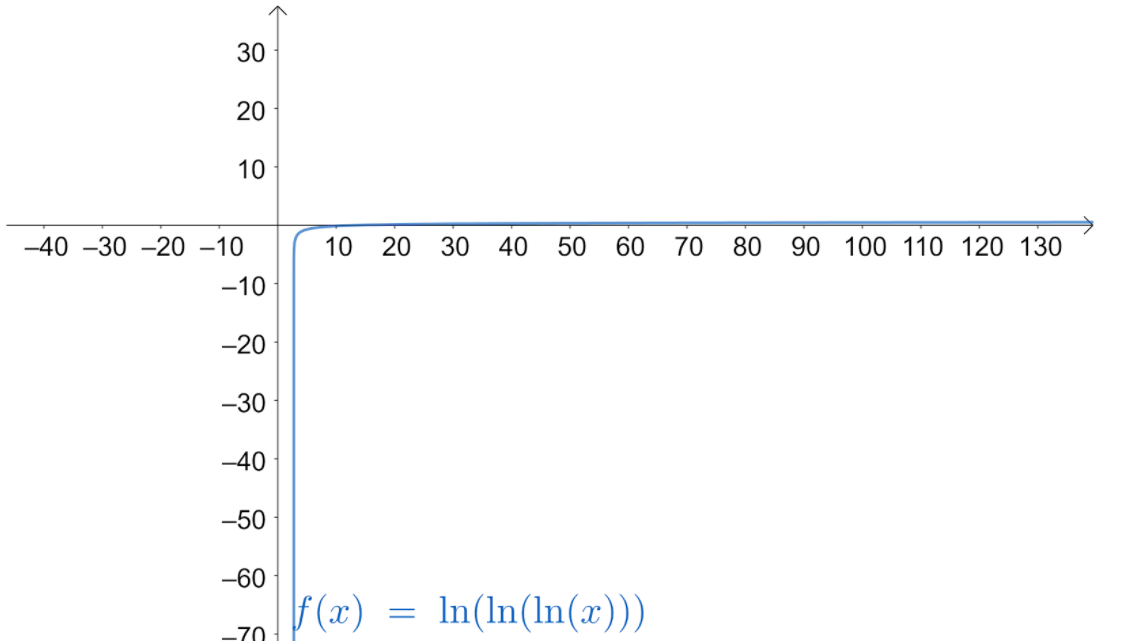
We can see that the function gives different values for different values of x and the range is R which makes the function one-one and onto.