Question
Question: If a direct current of value A ampere is superimposed on an alternating current \(I = b\sin \omega t...
If a direct current of value A ampere is superimposed on an alternating current I=bsinωt flowing through a wire, what is the effective (rms) value of the resulting current in the circuit?
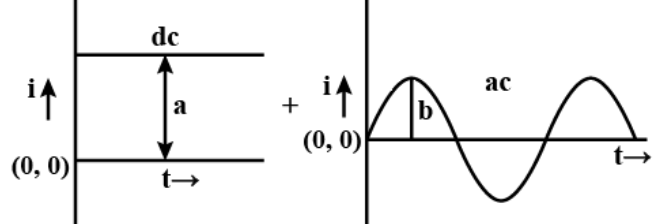
Solution
Hint – In order to solve this problem you need to use the general formula of rms current using AC and DC current both and solve to get the asked value.
Complete step-by-step solution -
Total current including both diagrams we get,
i=a+bsinωt.
By the definition of RMS value irms=T∫0Ti2dt
On putting the value of i and operating (a+b)2 formula on it we get,
irms=T∫0T(a2+b2sin2ωt+2absinωt)dt
We know,
\cos 2\theta = 1 - 2{\sin ^2}\theta \\\
{\sin ^2}\theta = \dfrac{{1 - \cos 2\theta }}{2} \\\
So, irms=T∫0T(a2+b2(21−cosωt)+2absinωt)dt
We know the average value of cosωt and sinωt is 0 over one time period.
So, irms=T∫0T(a2+(2b2))dt=T(a2+(2b2))T=a2+(2b2)
Hence the answer is a2+(2b2)A.
Note – Whenever you need to solve these types of problems you need to know that
irms=T∫0Ti2dt. Then we have to solve considering the time period as limit and get the value of rms current. Here we have considered both AC and DC current and got its rms value.
