Question

If a circle of radius R passes through the origin O and intersects the coordinate axes at $A$ and $B$ , then find the locus of the foot of perpendicular from $O$ on $AB$ .
(A) ${\left( {{x^2} + {y^2}} \right)^2} = 4R{x^2}{y^2}$
(B) $\left( {{x^2} + {y^2}} \right)\left( {x + y} \right) = {R^2}xy$
(C) ${\left( {{x^2} + {y^2}} \right)^3} = 4{R^2}{x^2}{y^2}$
(D) ${\left( {{x^2} + {y^2}} \right)^2} = 4{R^2}{x^2}{y^2}$

Answer 1

We will first find the slope of the foot perpendicular from $O$ on $AB$ . As we know that the product of slopes of two perpendicular lines is $- 1$ , using this we will find the slope of $AB$ and then the equation of line $AB$ . Then we will find the coordinates of $A$ and $B$ . At last, we will find the length of $AB$ and then equate it to the diameter of the circle to find the locus.

Complete step-by-step solution:

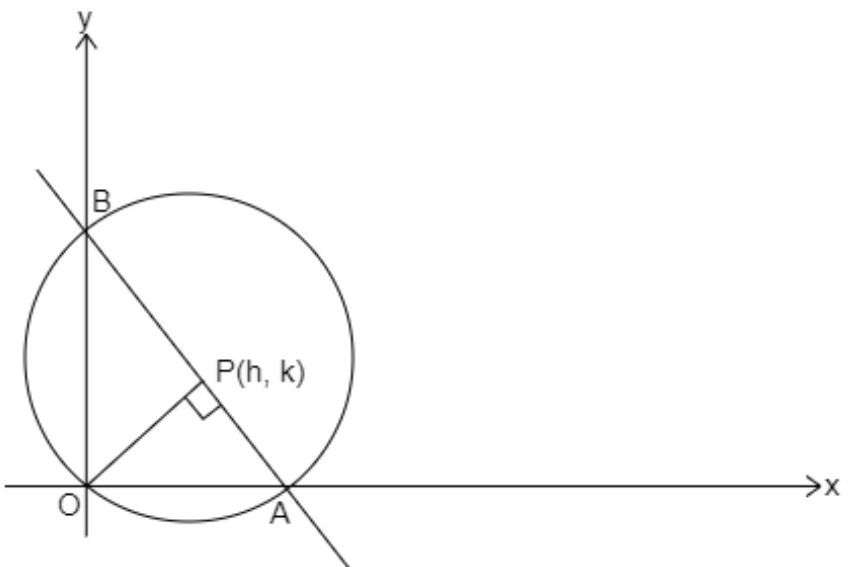
Let the foot of perpendicular from $O$ on $AB$ be $P(h,k)$ .
As $A$ lies on the x-axis, so the y coordinate of $A$ will be zero. Similarly, $B$ lies on the y-axis, so the x coordinate of $B$ will be zero.
Slope of OP$$$$ = \dfrac{{k - 0}}{{h - 0}}
$\therefore {\text{Slope of OP}} = \dfrac{k}{h}$
As $OP \bot AB$ ,
$\Rightarrow {\text{Slope of OP}} \times {\text{Slope of AB}} = - 1$
On solving, we get
$\Rightarrow \dfrac{k}{h} \times {\text{Slope of AB}} = - 1$
$\therefore {\text{Slope of AB}} = - \dfrac{h}{k}$
We know, equation of a line is given by
$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}(x - {x_1})$
Hence, equation of $AB$ is
$y - k = - \dfrac{h}{k}(x - h)$
Putting $x = 0$ ,
$y - k = \dfrac{{{h^2}}}{k}$
On rearranging,
$\Rightarrow y = \dfrac{{{k^2} + {h^2}}}{k}$
Now, putting $y = 0$ ,
$- k = - \dfrac{h}{k}\left( {x - h} \right)$
On solving,
$\Rightarrow \dfrac{{{k^2}}}{h} = \left( {x - h} \right)$
On rearranging,
$\Rightarrow x = \dfrac{{{k^2} + {h^2}}}{h}$
Now, we can write the coordinates of $A$ and $B$ as
$A\left( {\dfrac{{{k^2} + {h^2}}}{h},0} \right)$ and $B\left( {0,\dfrac{{{k^2} + {h^2}}}{k}} \right)$
Distance between two points $({x_1},{y_1})$ and $({x_2},{y_2})$ is given by $\sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}}$ .
$\therefore AB = \sqrt {{{\left( {\dfrac{{{k^2} + {h^2}}}{h} - 0} \right)}^2} + {{\left( {0 - \dfrac{{{k^2} + {h^2}}}{k}} \right)}^2}}$
$\because AB = 2R$
$\Rightarrow \sqrt {{{\left( {\dfrac{{{k^2} + {h^2}}}{h} - 0} \right)}^2} + {{\left( {0 - \dfrac{{{k^2} + {h^2}}}{k}} \right)}^2}} = 2R$
Squaring both sides
$\Rightarrow {\left( {\dfrac{{{k^2} + {h^2}}}{h}} \right)^2} + {\left( {\dfrac{{{k^2} + {h^2}}}{k}} \right)^2} = 4{R^2}$
On solving,
$\Rightarrow \dfrac{{{{\left( {{k^2} + {h^2}} \right)}^2}}}{{{h^2}}} + \dfrac{{{{\left( {{k^2} + {h^2}} \right)}^2}}}{{{k^2}}} = 4{R^2}$
Taking L.C.M.
$\Rightarrow \dfrac{{{k^2}{{\left( {{k^2} + {h^2}} \right)}^2} + {h^2}{{\left( {{k^2} + {h^2}} \right)}^2}}}{{{k^2}{h^2}}} = 4{R^2}$
Taking ${k^2}{h^2}$ to R.H.S.
$\Rightarrow {k^2}{\left( {{k^2} + {h^2}} \right)^2} + {h^2}{\left( {{k^2} + {h^2}} \right)^2} = 4{R^2}{k^2}{h^2}$
Taking ${\left( {{k^2} + {h^2}} \right)^2}$ common from L.H.S.
$\Rightarrow {\left( {{k^2} + {h^2}} \right)^2}\left( {{k^2} + {h^2}} \right) = 4{R^2}{k^2}{h^2}$
$\Rightarrow {\left( {{k^2} + {h^2}} \right)^3} = 4{R^2}{k^2}{h^2}$
Now, to find the locus we will replace $h$ with $x$ and $k$ with $y$ and rearrange,
$\Rightarrow {\left( {{x^2} + {y^2}} \right)^3} = 4{x^2}{y^2}{R^2}$
Therefore, the locus of the foot of perpendicular from $O$ on $AB$ is ${\left( {{x^2} + {y^2}} \right)^3} = 4{x^2}{y^2}{R^2}$ .
Hence, option (C) is correct.

Note: Centre of the circle and the foot of the perpendicular on the line $AB$ are two distinct points. One might get confused that the foot of the perpendicular is the centre of the circle and also $A$ lies on the x-axis, so the y coordinate of $A$ will be zero. Similarly, $B$ lies on the y-axis, so the x coordinate of $B$ will be zero.