Solveeit Logo
Login

Question

Question: If a circle of radius r is touching the lines \({x^2} - 4xy + {y^2} = 0\) in the first quadrant at p...

If a circle of radius r is touching the lines x2−4xy+y2=0{x^2} - 4xy + {y^2} = 0 in the first quadrant at points A and B, then the area of triangle OAB (O being the origin) is:
(1)33r24 (2)3r24 (3)3r24 (4)r2  (1)\dfrac{{3\sqrt 3 {r^2}}}{4} \\\ (2)\dfrac{{\sqrt 3 {r^2}}}{4} \\\ (3)\dfrac{{3{r^2}}}{4} \\\ (4){r^2} \\\

Explanation

Solution

Hint: Find the individual lines from the combined equation of the pair of straight lines and then find the angle between the lines. Then draw a diagram to find angles and lengths to find the area.

Complete step-by-step answer:
To find the individual equations from x2−4xy+y2=0{x^2} - 4xy + {y^2} = 0
Try to make square in one variable, by halving the coefficient of y and adding and subtracting the square of the halved term
y2−4xy+4x2−4x2+x2=0 (y−2x)2=3x2 y−2x=±3x  {y^2} - 4xy + 4{x^2} - 4{x^2} + {x^2} = 0 \\\ {(y - 2x)^2} = 3{x^2} \\\ y - 2x = \pm \sqrt 3 x \\\
So the two lines are,
L1: y=(2+3)xy = (2 + \sqrt 3 )x and L2: y=(2−3)xy = (2 - \sqrt 3 )x
m1=2+3 and m2=2−3{m_1} = 2 + \sqrt 3 {\text{ and }}{{\text{m}}_2} = 2 - \sqrt 3

Finding the angle between these lines using formula:
tan⁡θ=∣m2−m1∣1+m1m2\tan \theta = \dfrac{{|{m_2} - {m_1}|}}{{1 + {m_1}{m_2}}}
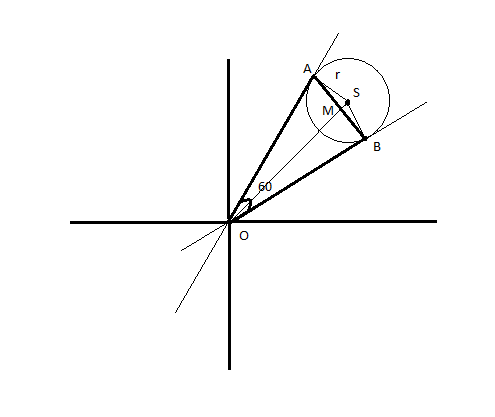
After substituting, we get tan⁡θ=3 so θ = π3=60∘\tan \theta = \sqrt 3 {\text{ so }}\theta {\text{ = }}\dfrac{\pi }{3} = {60^ \circ }

OS is the angle bisector of the internal angle between the lines OA and OB and it meets the centre of the circle.
We know that AS will be perpendicular to OA by the property that radius is always perpendicular to the tangent and the lines OA and OB are the tangents.
To find the area of ΔOAB\Delta OAB , let's find the area of ΔOAM\Delta OAM which we can find by taking the difference in the areas of ΔOAS and ΔAMS\Delta OAS{\text{ }}and{\text{ }}\Delta AMS .

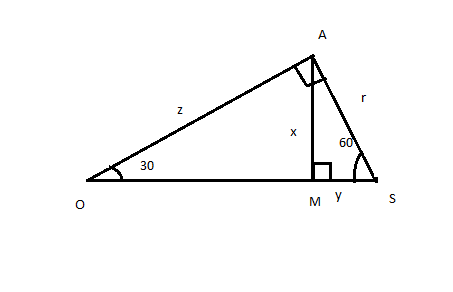
Area of
ΔOAS=12×z×r ΔAMS=12×x×y  \Delta OAS = \dfrac{1}{2} \times z \times r \\\ \Delta AMS = \dfrac{1}{2} \times x \times y \\\
Now, From
ΔOAS z=rtan⁡60∘ z=r3 ΔAMS x=rsin⁡60∘ x=r32 y=rcos⁡60∘ y=r2  \Delta OAS \\\ z = r\tan {60^ \circ } \\\ z = r\sqrt 3 \\\ \Delta AMS \\\ x = r\sin {60^ \circ } \\\ x = r\dfrac{{\sqrt 3 }}{2} \\\ y = r\cos {60^ \circ } \\\ y = \dfrac{r}{2} \\\
Area of ΔOAB=2×(ΔOAS−ΔAMS)\Delta OAB = 2 \times (\Delta OAS - \Delta AMS)
On putting the values in
ΔOAS=12×z×r ΔAMS=12×x×y  \Delta OAS = \dfrac{1}{2} \times z \times r \\\ \Delta AMS = \dfrac{1}{2} \times x \times y \\\
We get
2[×(12×r×3r)−(12×12r×32r)] =334r2  2[ \times (\dfrac{1}{2} \times r \times \sqrt 3 r) - (\dfrac{1}{2} \times \dfrac{1}{2}r \times \dfrac{{\sqrt 3 }}{2}r)] \\\ = \dfrac{{3\sqrt 3 }}{4}{r^2} \\\
Hence, option (1) is correct.

Note:
Deriving the individual equations from the combined equations should be known.
Properties of tangents are important in this case else the angles may go unnoticed and the question would become difficult to solve.