Question

If a circle of constant radius $3k$ passes through the origin and meets the axes at $A{\text{ and }}B$ , the locus of the centroid of $\Delta OAB$ is
A. ${x^2} + {y^2} = {k^2}$
B. ${x^2} + {y^2} = 2{k^2}$
C. ${x^2} + {y^2} = 3{k^2}$
D. None of these

Answer 1

Here we have the three points from where the circle is passing which are $(0,0)$ and the two points on the axes at $A{\text{ and }}B$ . Let $A = (a,0){\text{ and }}B = (0,b)$ . We need to find the locus of the centroid. So we can let it be $(m,n)$ and get the value of $m,n$ in the terms of given variables and then easily find the locus.

Complete step by step solution:
Here we are given that a circle of constant radius $3k$ passes through the origin and meets the axes at $A{\text{ and }}B$ and we need to find the locus of the centroid of $\Delta OAB$
So we know the general equation of the circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$ where centre of the circle is given by the point $\left( { - g, - f} \right)$ and the radius as $\sqrt {({g^2} + {f^2} - c)}$
So let us consider the general equation of the circle and proceed.

$C:{x^2} + {y^2} + 2gx + 2fy + c = 0$
Here we are given that the circle passes through origin. Hence $(0,0)$ will satisfy this equation.
${(0)^2} + {(0)^2} + 2g(0) + 2f(0) + c = 0$
$c = 0$
Hence we get the equation reduced to ${x^2} + {y^2} + 2gx + 2fy = 0$
We know that ${\text{Radius}} = \sqrt {({g^2} + {f^2} - c)} = \sqrt {({g^2} + {f^2})}$ as $c = 0$
We are given that ${\text{Radius}} = 3k$
So we can equate both and get:
$3k = \sqrt {({g^2} + {f^2})}$
Squaring both sides we get:
${g^2} + {f^2} = 9{k^2}$ $- - - - (1)$
Now we also know that $A$ is the point on the $x - {\text{axis}}$ hence at $A$ the value of $y = 0$
Putting $y = 0$ in the equation of the circle to get
${x^2} + {y^2} + 2gx + 2fy = 0$
${x^2} + {(0)^2} + 2gx + 2f(0) = 0 \\\ {x^2} + 2gx = 0 \\\$
$x(x + 2g) = 0$
So we can say that $x = 0, - 2g$
But we cannot take $x = 0$ as if we will take this then the point will come to be the origin whereas we need the point on the $x - {\text{axis}}$
Hence we get the value of $x = - 2g$
So we get the point $A = ( - 2g,0)$
Now we also know that $B$ is the point on the $y - {\text{axis}}$ hence at $B$ the value of $x = 0$
Putting $y = 0$ in the equation of the circle to get
${x^2} + {y^2} + 2gx + 2fy = 0$
${(0)^2} + {y^2} + 2g(0) + 2fy = 0 \\\ {y^2} + 2fy = 0 \\\$
$y(y + 2f) = 0$
So we can say that $y = 0, - 2f$
But we cannot take $y = 0$ as if we will take this then the point will come to be the origin whereas we need the point on the $y - {\text{axis}}$
Hence we get the value of $y = - 2f$
So we get the point $B = (0, - 2f)$
So we have three points that are $O(0,0),A( - 2g,0),B(0, - 2f)$
In $\Delta OAB$
Let the centroid be $(m,n)$
We know that if the three points of the triangle are $(a,b),(c,d),(e,f)$ then the centroid is given by $\left( {\dfrac{{a + c + e}}{3},\dfrac{{b + d + f}}{3}} \right)$
So we can say that
$m = \dfrac{{0 - 2g + 0}}{3} = \dfrac{{ - 2g}}{3}$
$n = \dfrac{{0 - 2f + 0}}{3} = \dfrac{{ - 2f}}{3}$
So we get that
$g = - \dfrac{{3m}}{2}$
$f = - \dfrac{{3n}}{2}$
Now substituting the value of $g,f$ in equation (1) we get
${\left( { - \dfrac{{3m}}{2}} \right)^2} + {\left( { - \dfrac{{3n}}{2}} \right)^2} = 9{k^2} \\\ \dfrac{{9{m^2}}}{4} + \dfrac{{9{n^2}}}{4} = 9{k^2} \\\$
${m^2} + {n^2} = 4{k^2}$
Now substituting $x = m,y = n$ as we need the locus of the centroid we get:
${x^2} + {y^2} = 4{k^2}$

Hence D is the correct option.

Note:
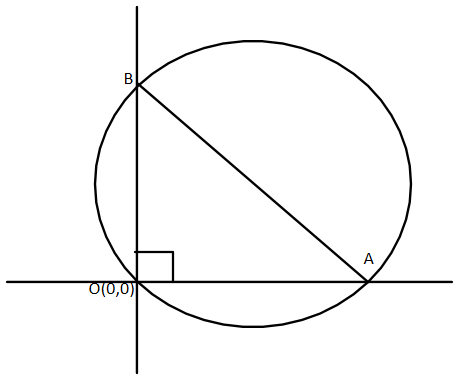
Here the student can also do this problem by the alternate way where we just need to proceed by the figure of the problem. Here we can let the point $A = (a,0),B = (0,b)$ and origin is known to us $O = (0,0)$
Hence we have all the three points. We know that centroid will be $\left( {\dfrac{{a + 0 + 0}}{3},\dfrac{{0 + b + 0}}{3}} \right) = \left( {\dfrac{a}{3},\dfrac{b}{3}} \right)$
Now we also know that $AB$ is the diameter of the circle as we know the property that the ends of the diameter make the angle of $90^\circ$ on any point on the circle. Hence we can say that $AB = 2({\text{radius)}} = 6k$
Now we can apply distance formula between $A{\text{ and }}B$
So we will get $\sqrt {{{\left( {\dfrac{a}{3}} \right)}^2} + {{\left( {\dfrac{b}{3}} \right)}^2}} = 6k$
From here also we will get the relation between $a{\text{ and }}b$ and hence we can solve both to get the locus of the centroid.