Question

If a circle C is passing through the point $\left( 4,0 \right)$ touches the circle ${{x}^{2}}+{{y}^{2}}+4x-6y=12$ externally at the point $\left( 1,-1 \right)$, then find the radius of the circle C?
(a) $\sqrt{57}$,
(b) 4,
(c) $2\sqrt{5}$,
(d) 5.

Answer 1

We use the fact that there will be a tangent passing through the point of intersection if the two circles are touching externally. We find the equation of the tangent of the circle ${{x}^{2}}+{{y}^{2}}+4x-6y=12$ at the point $\left( 1,-1 \right)$. We now use the fact that the equation of the circle touching another circle ${{x}^{2}}+{{y}^{2}}+ax+by+c=0$ externally at a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having tangent $lx+my+n=0$ passing through the same point is ${{x}^{2}}+{{y}^{2}}+ax+by+c+\alpha \left( lx+my+n \right)=0$ to get the equation of circle C. We substitute the point $\left( 4,0 \right)$ to solve for the value of $\alpha$ and to get the radius of the circle.

Complete step-by-step answer:
Given that we have a circle C that is passing through the point $\left( 4,0 \right)$ and touches the circle ${{x}^{2}}+{{y}^{2}}+4x-6y=12$ externally at the point $\left( 1,-1 \right)$. We need to find the radius of the given circle C.
Let us draw to represent all the given information.

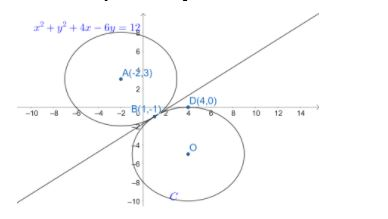
We know that if two circles are touching externally, then there will be a tangent passing through the point of intersection of the circles. Let us find equation of the tangent of the circle ${{x}^{2}}+{{y}^{2}}+4x-6y=12$ at the point $\left( 1,-1 \right)$.
We know that the slope of the given curve at a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is defined as ${{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$.
We have the equation of the circle ${{x}^{2}}+{{y}^{2}}+4x-6y=12$. We differentiate w.r.t x on both sides.
$\Rightarrow \dfrac{d}{dx}\left( {{x}^{2}}+{{y}^{2}}+4x-6y \right)=\dfrac{d}{dx}\left( 12 \right)$.
$\Rightarrow \dfrac{d}{dx}\left( {{x}^{2}} \right)+\dfrac{d}{dx}\left( {{y}^{2}} \right)+\dfrac{d}{dx}\left( 4x \right)-\dfrac{d}{dx}\left( 6y \right)=\dfrac{d}{dx}\left( 12 \right)$.
We know that $\dfrac{d}{dx}\left( {{x}^{2}} \right)=2x$, $\dfrac{d}{dx}\left( {{y}^{n}} \right)=n{{y}^{n-1}}\dfrac{dy}{dx}$, $\dfrac{d}{dx}\left( c \right)=0$ and $\dfrac{d}{dx}\left( ax \right)=a$.
$\Rightarrow 2x+2y\dfrac{dy}{dx}+4-6\dfrac{dy}{dx}=0$.
$\Rightarrow 2x+4+\left( 2y-6 \right)\dfrac{dy}{dx}=0$.
$\Rightarrow \left( 6-2y \right)\dfrac{dy}{dx}=2x+4$.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{2x+4}{6-2y}$.
Let the slope of the tangent be ‘m’.
$\Rightarrow m={{\left. \dfrac{dy}{dx} \right|}_{\left( 1,-1 \right)}}=\dfrac{2\left( 1 \right)+4}{6-2\left( -1 \right)}$.
$\Rightarrow m=\dfrac{2+4}{6+2}$.
$\Rightarrow m=\dfrac{6}{8}$.
$\Rightarrow m=\dfrac{3}{4}$.
We need to find the equation of the tangent with slope $m=\dfrac{3}{4}$ and passing through the point $\left( 1,-1 \right)$.
We know that the equation of the line passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ and having slope ‘m’ is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. We use this to find the equation of the tangent.
So, the equation of the tangent is $y-\left( -1 \right)=\dfrac{3}{4}\left( x-1 \right)$.
$\Rightarrow 4\left( y+1 \right)=3\left( x-1 \right)$.
$\Rightarrow 4y+4=3x-3$.
$\Rightarrow 3x-4y-4-3=0$.
$\Rightarrow 3x-4y-7=0$ ----(1).
We need to find the equation of the circle which touches ${{x}^{2}}+{{y}^{2}}+4x-6y-12=0$ externally and has a tangent $3x-4y-7=0$.
We know that the equation of the circle touching another circle ${{x}^{2}}+{{y}^{2}}+ax+by+c=0$ externally at a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having tangent $lx+my+n=0$ passing through the same point is .
${{x}^{2}}+{{y}^{2}}+ax+by+c+\alpha \left( lx+my+n \right)=0$. We use this result to find the equation of C.
We get the equation of the circle as ${{x}^{2}}+{{y}^{2}}+4x-6y-12+\alpha \left( 3x-4y-7 \right)=0$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}+4x-6y-12+3\alpha x-4\alpha y-7\alpha =0$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}+\left( 4+3\alpha \right)x+\left( -6-4\alpha \right)y-12-7\alpha =0$ ----(2).
According to the problem, the circle in equation (2) passes through the point $\left( 4,0 \right)$. So, we substitute the point $\left( 4,0 \right)$ in equation (2).
$\Rightarrow {{\left( 4 \right)}^{2}}+{{\left( 0 \right)}^{2}}+\left( 4+3\alpha \right)\left( 4 \right)+\left( -6-4\alpha \right)\left( 0 \right)-12-7\alpha =0$.
$\Rightarrow 16+0+16+12\alpha +0-12-7\alpha =0$.
$\Rightarrow 20+5\alpha =0$.
$\Rightarrow 5\alpha =-20$.
$\Rightarrow \alpha =\dfrac{-20}{5}$.
$\Rightarrow \alpha =-4$.
Let us substitute the value of $\alpha$ in equation (2).
$\Rightarrow {{x}^{2}}+{{y}^{2}}+\left( 4+3\left( -4 \right) \right)x+\left( -6-4\left( -4 \right) \right)y-12-7\left( -4 \right)=0$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}+\left( 4-12 \right)x+\left( -6+16 \right)y-12+28=0$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}-8x+10y+16=0$.
$\Rightarrow {{x}^{2}}-8x+16+{{y}^{2}}+10y+25=25$.
$\Rightarrow {{\left( x-4 \right)}^{2}}+{{\left( y+5 \right)}^{2}}={{5}^{2}}$ ---(3).
We know that if the equation of the circle is ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$, then the radius of the circle is r. We use this in equation (3) to get the radius of circle C as 5.
∴ The radius of the circle C is 5 units.

So, the correct answer is “Option d”.

Note: We can alternatively solve by assigning a center for the circle C and use the fact that distance between the centers is equal to the sum of radii of the two externally circles. We use the distance from center to any point on the circumference of the circle to get the coordinates of center of circle C. Using these coordinates, we can find the radius of the circle C. Similarly, we can expect problems to find the equation of the circle C.