Question
Question: If a capacitor between A and B is \[12\mu F\] the capacity C is? A. \[5\mu F\] B. \[3\mu F\] C...
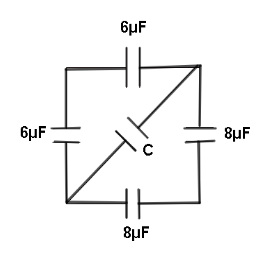
If a capacitor between A and B is 12μF the capacity C is?
A. 5μF
B. 3μF
C. 4μF
D. 8μF
Solution
we will solve this question by finding the equation of total capacitance of the circuit. Both 6μF capacitors are in series. Both 8μF capacitors are also in series with each other. And the unknown capacity C is in parallel with them. The equivalent capacitance has been given to us, thus we will equate the given capacitance to the equivalent capacitance found by us after applying the formulas.
Formula used:
Equivalent capacitance of 2 capacitors in series is given by:
Ceq1=C11+C21
Equivalent capacitance of 2 capacitors in parallel is given by:
Ceq=C1+C2
Complete step by step answer:
Look at the diagram below to get a better idea:
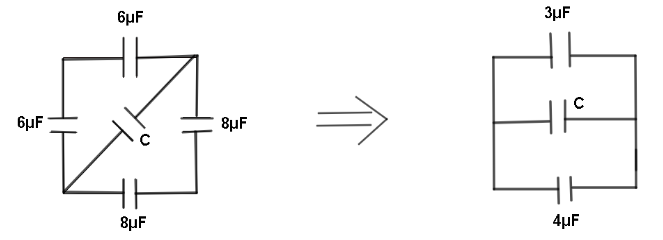
Let us start solving the question by finding equivalent capacitance of 6μF in series:
Ceq1=C11+C21
⇒Ceq1=61+61
⇒Ceq1=62
⇒Ceq1=31
⇒Ceq=3μF
Now we will find equivalent capacitance of 8μF capacitors:
Ceq1=C11+C21
⇒Ceq1=81+81
⇒Ceq1=82
⇒Ceq1=41
⇒Ceq=4μF.
Now these 3 capacitors Ceq=4μF, Ceq=3μF and CμF are in parallel connection. Hence now we will apply the formula for equivalent capacitance of capacitors in parallel.
Ceq=C1+C2+C3
⇒Ceq=C+3+4
⇒Ceq=C+7
It has been mentioned that equivalent capacitance is 12μF.
Hence we will substitute Ceq=12
12=C+7
⇒C=12−7μF
∴C=5μF.
Hence the capacity of capacitor C is 5μF.
Hence the correct answer is option A.
Note: Always remember that the formula for equivalent capacitance in series and parallel combination of capacitors is opposite to the formula of resistors. We said that the 6μF and 8μF capacitors are in series because the potential across the ends of capacitors is different. And later 8μF, 6μF and C are said to be parallel because the potential difference across their ends is the same.
