Solveeit Logo
Login

Question

Question: If a boat can have a speed of \(4{\text{ km}}\,{\text{h}}{{\text{r}}^{{\text{ - 1}}}}\) in still wat...

If a boat can have a speed of 4 km hr - 14{\text{ km}}\,{\text{h}}{{\text{r}}^{{\text{ - 1}}}} in still water, for what values of speed of river flow, it can be managed to row boat right across the river, without any drift?
A. ⩾4km hr - 1\geqslant {\text{4km}}\,{\text{h}}{{\text{r}}^{{\text{ - 1}}}}
B. Greater than zero but less than 4km hr - 14{\text{km}}\,{\text{h}}{{\text{r}}^{{\text{ - 1}}}}
C. Only 4km hr - 14{\text{km}}\,{\text{h}}{{\text{r}}^{{\text{ - 1}}}}
D. None of these

Explanation

Solution

First we have to draw a rough diagram showing all the speed, speed of river, speed of boat of and speed of boat with respect to the river speed. Now assume a speed for the river and then write the components of the speed of the boat with respect to the river then after do some rearrangement and equate the x-component to zero as there is no drift. Then we will find our solution.

Complete step by step answer:
As per the problem, a boat can have a speed of 4km hr - 14{\text{km}}\,{\text{h}}{{\text{r}}^{{\text{ - 1}}}} in still water. We need to find the speed of river flow so that it can manage to row boats right across the river, without any drift.

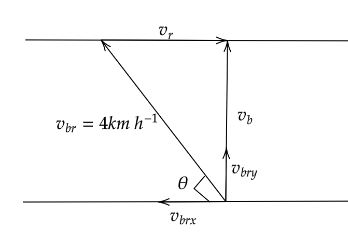
Now the boat is moving at an angle of θ\theta opposite to the direction of speed of the river.Let us take the x-direction of the boat to be positive and the river to be opposite to it.Hence,
vbr=4km h - 1{v_{br}} = 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}
Now splitting the speed of the boat with respect to river into two components we will get,
vbr=vbrx+vbry=vbrcos⁡θ i+vbrsin⁡θ j{v_{br}} = {v_{brx}} + {v_{bry}} = {v_{br}}\cos \theta {\text{ i}} + {v_{br}}\sin \theta {\text{ j}}
Now putting the value we will get,
vbr=4km h - 1cos⁡θ i+4km h - 1sin⁡θ j{v_{br}} = 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\cos \theta {\text{ i}} + 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\sin \theta {\text{ j}}

We can say, vbr=vb−vr{v_{br}} = {v_b} - {v_r}
Now on putting above we will get,
vb−vr=4km h - 1cos⁡θ i+4km h - 1sin⁡θ j……(1){v_b} - {v_r} = 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\cos \theta {\text{ i}} + 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\sin \theta {\text{ j}} \ldots \ldots \left( 1 \right)
Now let us assume the speed of the river be,
vr=−v i{v_r} = - v\,{\text{i}}
Now putting speed of river in place of equation (1)\left( 1 \right) we will get,
vb−(−v i)=4km h - 1cos⁡θ i+4km h - 1sin⁡θ j{v_b} - \left( { - v\,{\text{i}}} \right) = 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\cos \theta {\text{ i}} + 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\sin \theta {\text{ j}}

Rearranging the equation we will get,
vb=4km h - 1cos⁡θ i−v i+4km h - 1sin⁡θ j{v_b} = 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\cos \theta {\text{ i}} - v{\text{ i}} + 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\sin \theta {\text{ j}}
Speed of the boat for zero drift the x-component should be zero.Hence,
4km h - 1cos⁡θ −v = 04{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\cos \theta {\text{ }} - v{\text{ = 0}}
⇒4km h - 1cos⁡θ = v\Rightarrow 4{\text{km}}\,{{\text{h}}^{{\text{ - 1}}}}\cos \theta {\text{ = }}v
So we can say the speed of the river should be,
∴0<v<4km h−1\therefore0 < v < 4{\text{km }}{{\text{h}}^{ - 1}}

Therefore the correct option is B.

Note: Drift is distance along a river that a boat covers while crossing the river.Remember that when a boat is moving with a speed in still water then it is the speed of the boat with respect to the speed of the river. Another important formula for speed of boat in still water is defined as half the sum of downstream speed and upstream speed.