Solveeit Logo
Login

Question

Question: If $A = \begin{bmatrix} 2 & 2 \\ -3 & 2 \end{bmatrix}$, $B = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bm...

If A=[22−32]A = \begin{bmatrix} 2 & 2 \\ -3 & 2 \end{bmatrix}, B=[0−110]B = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} then (B−1A−1)−1=(B^{-1}A^{-1})^{-1} =

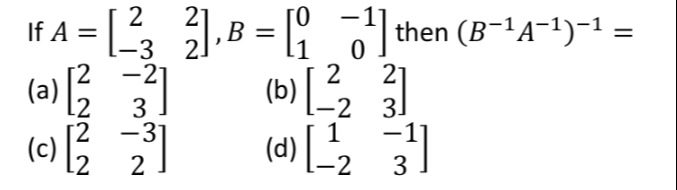
A

[2−223]\begin{bmatrix} 2 & -2 \\ 2 & 3 \end{bmatrix}

B

[22−23]\begin{bmatrix} 2 & 2 \\ -2 & 3 \end{bmatrix}

C

[2−322]\begin{bmatrix} 2 & -3 \\ 2 & 2 \end{bmatrix}

D

[1−1−23]\begin{bmatrix} 1 & -1 \\ -2 & 3 \end{bmatrix}

Answer

[2−223]\begin{bmatrix} 2 & -2 \\ 2 & 3 \end{bmatrix}

Explanation

Solution

To find (B−1A−1)−1(B^{-1}A^{-1})^{-1}, we can use the property that (XY)−1=Y−1X−1(XY)^{-1} = Y^{-1}X^{-1}. Therefore, (B−1A−1)−1=(A−1)−1(B−1)−1(B^{-1}A^{-1})^{-1} = (A^{-1})^{-1}(B^{-1})^{-1}.

Also, (A−1)−1=A(A^{-1})^{-1} = A and (B−1)−1=B(B^{-1})^{-1} = B. Thus, (B−1A−1)−1=AB(B^{-1}A^{-1})^{-1} = AB.

Now, we compute the matrix product ABAB:

AB=[22−32][0−110]=[(2)(0)+(2)(1)(2)(−1)+(2)(0)(−3)(0)+(2)(1)(−3)(−1)+(2)(0)]=[2−223]AB = \begin{bmatrix} 2 & 2 \\ -3 & 2 \end{bmatrix} \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} (2)(0)+(2)(1) & (2)(-1)+(2)(0) \\ (-3)(0)+(2)(1) & (-3)(-1)+(2)(0) \end{bmatrix} = \begin{bmatrix} 2 & -2 \\ 2 & 3 \end{bmatrix}.

Therefore, (B−1A−1)−1=[2−223](B^{-1}A^{-1})^{-1} = \begin{bmatrix} 2 & -2 \\ 2 & 3 \end{bmatrix}.