Question
Question: If $A = \begin{bmatrix} 2 & -1 \\ 4 & -2 \end{bmatrix}$, then the value of $det(I+2A+3A^2+4A^3+5A^4+...
If A=[24−1−2], then the value of det(I+2A+3A2+4A3+5A4+…upto∞) is
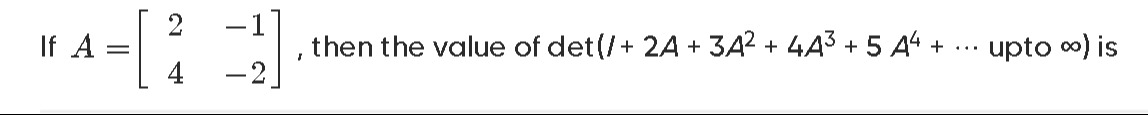
1
Solution
The given series is S=I+2A+3A2+4A3+5A4+…upto∞. This is a matrix power series. We can relate it to a known scalar series. Consider the scalar geometric series: G(x)=1+x+x2+x3+⋯=1−x1 for ∣x∣<1. Differentiating G(x) with respect to x: dxdG(x)=0+1+2x+3x2+⋯=∑n=1∞nxn−1. Also, dxd(1−x)−1=−1(1−x)−2(−1)=(1−x)−2. Thus, the sum of the scalar series S(x)=1+2x+3x2+4x3+… is (1−x)−2 for ∣x∣<1.
Extending this to matrices, the sum of the matrix series S=I+2A+3A2+4A3+… is (I−A)−2, provided the series converges. The convergence condition for such a series is that the spectral radius of matrix A, denoted ρ(A), must be less than 1. The spectral radius is the maximum magnitude of the eigenvalues of A.
Step 1: Find the eigenvalues of matrix A to check for convergence. Given A=[24−1−2]. The characteristic equation is det(A−λI)=0. det[2−λ4−1−2−λ]=0 (2−λ)(−2−λ)−(−1)(4)=0 −(4−λ2)+4=0 −4+λ2+4=0 λ2=0 The eigenvalues are λ1=0 and λ2=0. The spectral radius ρ(A)=max(∣λ1∣,∣λ2∣)=max(∣0∣,∣0∣)=0. Since ρ(A)=0<1, the series converges, and its sum is S=(I−A)−2.
Step 2: Calculate I−A. I−A=[1001]−[24−1−2]=[1−20−40−(−1)1−(−2)]=[−1−413].
Step 3: Calculate the determinant of I−A. det(I−A)=(−1)(3)−(1)(−4)=−3−(−4)=−3+4=1.
Step 4: Calculate the determinant of the series sum S=(I−A)−2. Using the properties of determinants: det(Mk)=(det(M))k and det(M−1)=det(M)1. Therefore, det(S)=det((I−A)−2)=(det((I−A)−1))2=(det(I−A)1)2. Substitute the value of det(I−A): det(S)=(11)2=12=1.
The final answer is 1.
Explanation of the solution:
- Recognize the given infinite series as S=∑n=1∞nAn−1.
- Recall that the scalar series 1+2x+3x2+… sums to (1−x)−2 for ∣x∣<1.
- Extend this to matrices: S=(I−A)−2, provided the spectral radius ρ(A)<1.
- Calculate the eigenvalues of A: λ2=0⟹λ=0. So ρ(A)=0<1, confirming convergence.
- Calculate I−A=[−1−413].
- Calculate det(I−A)=(−1)(3)−(1)(−4)=1.
- Use the determinant property det((I−A)−2)=(det(I−A)−1)2=(det(I−A)1)2.
- Substitute det(I−A)=1 to get det(S)=(11)2=1.
