Solveeit Logo
Login

Question

Question: If $A = \begin{bmatrix} 1 & \tan x \\ -\tan x & 1 \end{bmatrix}$, then the value of $|A'A^{-1}|$ is...

If A=[1tan⁡x−tan⁡x1]A = \begin{bmatrix} 1 & \tan x \\ -\tan x & 1 \end{bmatrix}, then the value of ∣A′A−1∣|A'A^{-1}| is

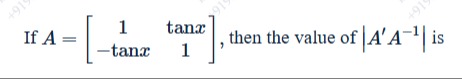
A

-1

B

0

C

1

D

2

Answer

1

Explanation

Solution

Using determinant properties, ∣A′A−1∣=∣A′∣∣A−1∣|A'A^{-1}| = |A'| |A^{-1}|. Since ∣A′∣=∣A∣|A'| = |A| and ∣A−1∣=1/∣A∣|A^{-1}| = 1/|A| (as ∣A∣=1+tan⁡2x=sec⁡2x≠0|A| = 1+\tan^2 x = \sec^2 x \neq 0), we have ∣A′A−1∣=∣A∣⋅(1/∣A∣)=1|A'A^{-1}| = |A| \cdot (1/|A|) = 1.