Question
Question: If $A = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}$ and $B = \begin{bmatrix} -5 & 4 & 0 \\ 0 & 2 & -1...
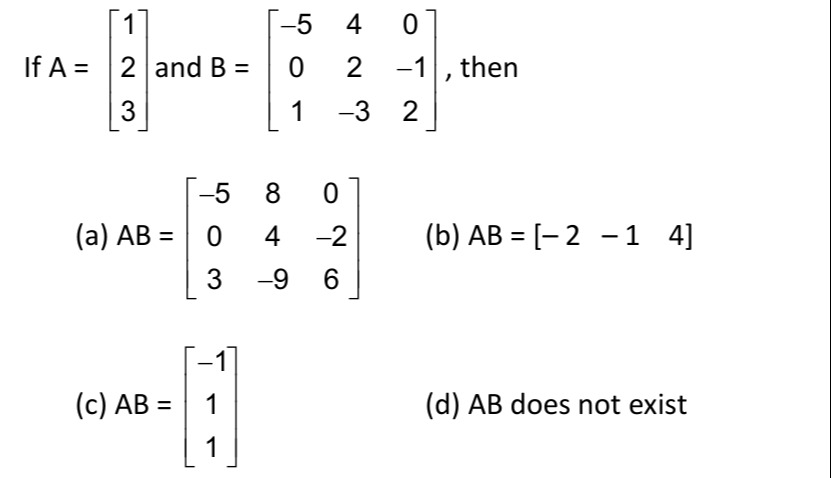
If A=123 and B=−50142−30−12, then
A
AB=−50384−90−26
B
AB=[−2 −1 4]
C
AB=−111
D
AB does not exist
Answer
AB does not exist
Explanation
Solution
Matrix A has dimensions 3×1. Matrix B has dimensions 3×3. For the matrix product AB to be defined, the number of columns in A must equal the number of rows in B. The number of columns in A is 1, and the number of rows in B is 3. Since 1=3, the product AB is not defined.
