Question

if $A = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}$ and $M = A + A^2 + A^3 + ... + A^{20}$, then the sum of all the elements of the matrix $M$ is equal to ____.

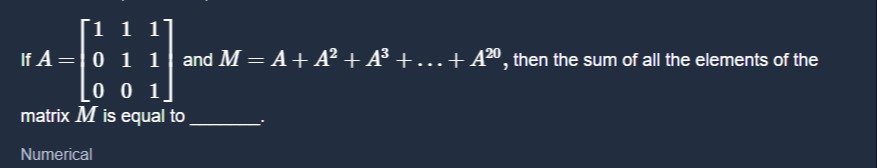
Answer 1

2020

Answer 2

We are given

$$A=\begin{bmatrix}1 & 1 & 1\\0 & 1 & 1\\0 & 0 & 1\end{bmatrix}.$$

Notice that $A = I + N$ where

$$N=\begin{bmatrix}0 & 1 & 1\\0 & 0 & 1\\0 & 0 & 0\end{bmatrix}\quad\text{with}\quad N^3=0.$$

By the binomial theorem for matrices,

$$A^n=(I+N)^n = I + nN + \binom{n}{2}N^2.$$

Since

$$N^2=\begin{bmatrix}0 & 0 & 1\\0 & 0 & 0\\0 & 0 & 0\end{bmatrix},$$

we have

$$A^n = \begin{bmatrix} 1 & n & n+\binom{n}{2} \\[1mm] 0 & 1 & n \\[1mm] 0 & 0 & 1 \end{bmatrix}.$$

Sum of elements of $A^n$:

• Row 1: $1 + n + \left(n+\binom{n}{2}\right) = 1 + 2n + \binom{n}{2}$.
• Row 2: $0 + 1 + n = 1+n$.
• Row 3: $0+0+1 = 1$.

Total of $A^n$:

$$S(n)=\Big[1+2n+\binom{n}{2}\Big] + (1+n) + 1 = 3+3n+\binom{n}{2},$$

where $\binom{n}{2}=\frac{n(n-1)}{2}$.

Matrix $M$ is:

$$M=A+A^2+\cdots+A^{20}.$$

Thus, total sum of elements in $M$ is

$$\sum_{n=1}^{20}\left(3+3n+\frac{n(n-1)}{2}\right).$$

Break into parts:

1. Constant term: $\sum_{n=1}^{20} 3 = 3 \times 20=60.$

2. Linear term: $\sum_{n=1}^{20}3n=3\left(\frac{20 \times 21}{2}\right)=3\times210=630.$

3. Quadratic term:

   $$\sum_{n=1}^{20}\frac{n(n-1)}{2} = \frac{1}{2}\sum_{n=1}^{20}(n^2-n).$$

   We know:

   $$\sum_{n=1}^{20} n^2 = \frac{20\cdot21\cdot41}{6} = 2870,\quad \sum_{n=1}^{20} n = 210.$$

   So,

   $$\frac{1}{2}(2870-210)=\frac{2660}{2}=1330.$$

Adding these,

$$\text{Total Sum} = 60 + 630 + 1330 = 2020.$$